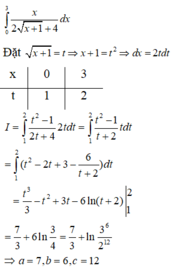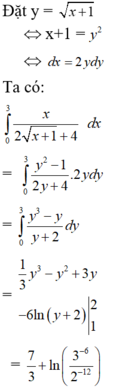cho a3+8b3 = 1 - 6ab. tính a+2b
NP
Những câu hỏi liên quan
Cho \(a>0\) , \(b>0\) thỏa mãn: \(\log_{3a+2b+1}\left(9a^2+b^2+1\right)+\log_{6ab+1}\left(3a+2b+1\right)=2\) .
Tính giá trị của biểu thức: \(P=a+2b\)
\(a;b>0\Rightarrow3a+2b+1>1\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\) đồng biến
Mà \(9a^2+b^2\ge2\sqrt{9a^2b^2}=6ab\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge2\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}log_{6ab+1}\left(3a+2b+1\right)=1\\3a=b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6ab+1=3a+2b+1\\b=3a\end{matrix}\right.\)
\(\Rightarrow18a^2+1=3a+6a+1\)
\(\Leftrightarrow18a^2-9a=0\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho hai số \(a,b\) thỏa mãn \(a+b=1\). Hãy tính giá trị của biểu thức
\(P=2a^3+6ab+2b^3-2024\)
\(P=2a^3+2b^3+6ab-2024\)
\(=2\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]+6ab-2024\)
\(=2\left[1-3ab\left(a+b\right)\right]+6ab-2024\)
\(=2-6ab+6ab-2024\)
=-2022
Đúng 0
Bình luận (1)
Cho
∫
0
3
x
2
x
+
1
+
4
d
x
a
3
+
ln
3
b
2
c
Tính T a+2b-c A. T...
Đọc tiếp
Cho ∫ 0 3 x 2 x + 1 + 4 d x = a 3 + ln 3 b 2 c Tính T = a+2b-c
A. T = 7
B. T = -7
C. T = 6
D. T = -6
Cho
∫
0
3
x
2
x
+
1
+
4
d
x
a
3
+
ln
(
3
b
2
c
)
Tính a+2b-c ...
Đọc tiếp
Cho ∫ 0 3 x 2 x + 1 + 4 d x = a 3 + ln ( 3 b 2 c ) Tính a+2b-c
A. T = 7
B. T = -7
C. T = 6
D. T = -6
Cho
∫
0
3
x
2
x
+
1
+
4
d
x
a
3
+
ln
(
3
b
2
c
)
Tính Ta+2b-c
Đọc tiếp
Cho ∫ 0 3 x 2 x + 1 + 4 d x = a 3 + ln ( 3 b 2 c ) Tính T=a+2b-c
![]()
![]()
![]()
![]()
Viết các biểu thức dưới dạng bình phương của 1 tổng hoặc 1 hiệu :
\(\dfrac{8}{27}\)a3 - \(\dfrac{8}{3}\)a2b + 8b2a - 8b3
xl chuyển hộ mk "bình phương" thành "lập phương" nha
Đúng 0
Bình luận (0)
\(=\left(\dfrac{2}{3}a\right)^3-3.\left(\dfrac{2}{3}\right)^2a^2.2b+3.\dfrac{2}{3}a.4b^2-\left(2b\right)^3=\left(\dfrac{2}{3}a-2b\right)^3\)
Đúng 0
Bình luận (0)
Cho a, b thỏa mãn:
2a2+9b2+6ab-14a-30b+29=0
Tính P=(1-a)2013 - (3-2b)2013
Cho a, b thỏa mãn:
2a2+9b2+6ab-14a-30b+29=0
Tính P=(1-a)2013 - (3-2b)2013
Giúp e vs ạ!! E cảm ơn trc ^^
Bài 1: chỉ ra chỗ sai của một trong hai vế và sửa lại cho đúng các hằng dẳng thức
a) x^2 - 2xy + 4y^2 = (x - 2y)^2
b) a^2 + 24ab + b^2 = (4a + 3b)^2
c) 9x^2 + 6xy + y^2 = (3x - y)^2
d) a^3 - 8a^2b + 6ab^2 - 8b^3 = (a - 2b)^3