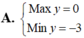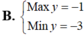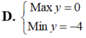Max y=9-sin2 3x-\(\sqrt{2}\)cos 3x
Max y= 3sin 3x -8 cos2 3x +4
giúp em với ạ
tìm max, min
a) y=\(\dfrac{\sqrt{x-1}}{x}\) trên \([1;5]\)
b) y=\(\dfrac{x+3}{\sqrt{x^2+1}}\) trên \([1;3]\)
c) y=\(\sin^2x-\cos x+1\)
d) y=\(\sin^3x-3\sin^2x+2\)
a0
a.
\(y'=\dfrac{2-x}{2x^2\sqrt{x-1}}=0\Rightarrow x=2\)
\(y\left(1\right)=0\) ; \(y\left(2\right)=\dfrac{1}{2}\) ; \(y\left(5\right)=\dfrac{2}{5}\)
\(\Rightarrow y_{min}=y\left(1\right)=0\)
\(y_{max}=y\left(2\right)=\dfrac{1}{2}\)
b.
\(y'=\dfrac{1-3x}{\sqrt{\left(x^2+1\right)^3}}< 0\) ; \(\forall x\in\left[1;3\right]\Rightarrow\) hàm nghịch biến trên [1;3]
\(\Rightarrow y_{max}=y\left(1\right)=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)
\(y_{min}=y\left(3\right)=\dfrac{6}{\sqrt{10}}=\dfrac{3\sqrt{10}}{5}\)
c.
\(y=1-cos^2x-cosx+1=-cos^2x-cosx+2\)
Đặt \(cosx=t\Rightarrow t\in\left[-1;1\right]\)
\(y=f\left(t\right)=-t^2-t+2\)
\(f'\left(t\right)=-2t-1=0\Rightarrow t=-\dfrac{1}{2}\)
\(f\left(-1\right)=2\) ; \(f\left(1\right)=0\) ; \(f\left(-\dfrac{1}{2}\right)=\dfrac{9}{4}\)
\(\Rightarrow y_{min}=0\) ; \(y_{max}=\dfrac{9}{4}\)
d.
Đặt \(sinx=t\Rightarrow t\in\left[-1;1\right]\)
\(y=f\left(t\right)=t^3-3t^2+2\Rightarrow f'\left(t\right)=3t^2-6t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=2\notin\left[-1;1\right]\end{matrix}\right.\)
\(f\left(-1\right)=-2\) ; \(f\left(1\right)=0\) ; \(f\left(0\right)=2\)
\(\Rightarrow y_{min}=-2\) ; \(y_{max}=2\)
Tìm MAX của :
A= \(3x\sqrt{8-3x^2}\)
Lời giải:
$A^2=9x^2(8-3x^2)=3.3x^2(8-3x^2)\leq 3.\left(\frac{3x^2+8-3x^2}{2}\right)^2=3.4^2$ (theo BĐT AM-GM)
$\Rightarrow A\leq 4\sqrt{3}$
Vậy $A_{\max}=4\sqrt{3}$. Giá trị này đạt tại $x=\frac{2}{\sqrt{3}}$
Tìm Max, Min của hàm số:
1) \(y=\dfrac{x+1+\sqrt{x-1}}{x+1+2\sqrt{x-1}}\)
2) \(y=\sin^{2016}x+\cos^{2016}x\)
3) \(y=2\cos x-\dfrac{4}{3}\cos^3x\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
4) \(y=\sin2x-\sqrt{2}x+1,x\in\left[0;\dfrac{\pi}{2}\right]\)
5) \(y=\dfrac{4-cos^2x}{\sqrt{sin^4x+1}},x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{3}\right]\)
tìm MAX P=\(-3x^2-4x\sqrt{y}+16x-2y+12\sqrt{y}+1999\)
\(P=-3x^2-4x\sqrt{y}+16x--y+12\sqrt{y}+1999\)
\(=-2\left(x^2+2x\sqrt{y}+y\right)+12\left(x+\sqrt{y}\right)-18-x^2+4x-4+2021\)
\(=-2\left(x+\sqrt{y}\right)^2+12\left(x+\sqrt{y}\right)-18-\left(x-2\right)^2+2021\)
\(=-2\left(x+\sqrt{y}-3\right)^2-\left(x-2\right)^2+2021\)\(\le2021\) với mọi x và y không âm
Dấu = xảy ra <=> x=2 và y=1
Vậy maxP=2021
Tìm Min,Max của các hàm số
a/ y= 2sin bình x+ cos bình 2x+2
b/ y=4sin2x + 5cos2x -2
c/ y= 3sin(2x-(pi/3))-2cos(2x-(pi/3))+1
d/ y=(2sin bình 3x+4sin3x.cos3x+1)/(sin6x+4cos6x+10)
Giusp mình với ạ!!! Thực sự mình rất cầN!!! Mình cảm ơn!
1) Cho x,y > 0 thoả mãn : 1/x + 1/y =1/2 Tìm min : A = \(\sqrt{x}+\sqrt{y}\)
2) Tìm min max B = \(\sqrt{3x-5}+\sqrt{7-3x}\)
1) \(\frac{1}{2}=\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)\(\Leftrightarrow\)\(x+y\ge8\)
\(\frac{1}{2}=\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}\)\(\Leftrightarrow\)\(xy=2\left(x+y\right)\ge16\)
\(A=\sqrt{x}+\sqrt{y}\ge2\sqrt[4]{xy}\ge2\sqrt[4]{16}=4\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y=4\)
2) \(B=\sqrt{3x-5}+\sqrt{7-3x}\ge\sqrt{3x-5+7-3x}=\sqrt{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(\orbr{\begin{cases}x=\frac{5}{3}\\x=\frac{7}{3}\end{cases}}\)
\(B=\sqrt{3x-5}+\sqrt{7-3x}\le\frac{3x-5+1+7-3x+1}{2}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=2\)
Bài 1: Tìm min max của các bthuc sau
a,A=\(\sqrt{x-2}+\sqrt{6-x}\)
b,B= \(\sqrt{2x+3}+\sqrt{13-2x}\)
c.,C=\(\sqrt{3x+9}+\sqrt{7-3x}\)
a) \(A=\sqrt{x-2}+\sqrt{6-x}\)
\(\Rightarrow A^2=x-2+6-x+2\sqrt{\left(x-2\right)\left(6-x\right)}\)
Ta có \(\sqrt{\left(x-2\right)\left(6-x\right)}\ge0,\forall x\)
Do đó \(A^2=4+2\sqrt{\left(x-2\right)\left(6-x\right)}\ge4\)
Mà A không âm \(\Leftrightarrow A\ge2\)
Dấu "=" \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)
Áp dụng BĐT Bunhiacopxky:
\(A^2=\left(\sqrt{x-2}+\sqrt{6-x}\right)^2\le\left(x-2+6-x\right)\left(1+1\right)=4\cdot2=8\)
\(\Leftrightarrow A\le\sqrt{8}\)
Dấu "=" \(\Leftrightarrow x-2=6-x\Leftrightarrow x=4\)
Mấy bài còn lại y chang nha
Tick hộ nha
a) Tìm max của T=\(\sqrt{3x-5}+\sqrt{7-3x}\)
b) Tìm nghiệm nguyên: \(x^2-25=y\left(y+6\right)\)
a. ĐKXĐ: \(\frac{5}{3}\le x\le\frac{7}{3}\)
Áp dụng BĐT Bunhiacopxki:
\(T^2=\left(\sqrt{3x-5}+\sqrt{7-3x}\right)\)
\(\le\left(1+1\right)\left(3x-5+7-3x\right)=4\)
\(\Rightarrow T\le2\left(\text{Vì }T>0\right)\)
b.
\(x^2-25=y\left(y+6\right)\)
\(\Leftrightarrow x^2-y^2-6y-9=16\)
\(\Leftrightarrow x^2-\left(y+3\right)^2=16\)
\(\Leftrightarrow\left(x-y-3\right)\left(x+y+3\right)=16=1.16=\left(-1\right)\left(-16\right)=2.8=\left(-2\right)\left(-8\right)\)
TH1: \(\left\{{}\begin{matrix}x-y-3=1\\x+y+3=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{17}{2}\\y=\frac{21}{2}\end{matrix}\right.\left(l\right)\)
TH2: \(\left\{{}\begin{matrix}x-y-3=-1\\x+y+3=-16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\frac{17}{2}\\y=-\frac{11}{2}\end{matrix}\right.\left(l\right)\)
TH3: \(\left\{{}\begin{matrix}x-y-3=2\\x+y+3=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=7\end{matrix}\right.\)
TH4: \(\left\{{}\begin{matrix}x-y-3=-2\\x+y+3=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=-6\end{matrix}\right.\)
TH5: \(\left\{{}\begin{matrix}x-y-3=16\\x+y+3=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{17}{2}\\y=-\frac{21}{2}\end{matrix}\right.\left(l\right)\)
TH6: \(\left\{{}\begin{matrix}x-y-3=-16\\x+y+3=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\frac{17}{2}\\y=\frac{9}{2}\end{matrix}\right.\left(l\right)\)
TH7: \(\left\{{}\begin{matrix}x-y-3=-8\\x+y+3=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=0\end{matrix}\right.\)
TH8: \(\left\{{}\begin{matrix}x-y-3=8\\x+y+3=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-6\end{matrix}\right.\)
thử lại
Vậy pt đã cho có nghiệm ...
Tìm GTLN, GTNN (Max,Min) của y = x 2 - 3 x + 3 x - 2 khi x ∈ 0 ; 3