cho hình vẽ . chứng minh AB song song với CD B A E C D 100 độ 120 độ 140 độ
TH
Những câu hỏi liên quan
Cho tam giác ABC, có góc A = 70 độ. Vẽ góc B, C là góc nhọn. Vẽ BD vuông góc với AC ( D thuộc AC ), Vẽ CE vuông góc với AB ( E thuộc AB ). Vẽ Bx song song với CE, vẽ CI song song với CD, Vẽ CI song song với BD.
a. Chứng minh AB vuông góc với Bx
b. Chứng minh Ac vuông góc với CI
cho hình thang biết : A = C = 100 độ; D = 80 độ
Chứng tỏ ; a, AB song song CD
b. AD song song BC
Cho hình vẽ biết góc a bằng 120 độ góc B bằng 60 độ góc C bằng 30 độ Chứng minh a b song song với BC Tính góc ABC và góc x DC
Bạn vào trang học 24 để tham khảo nha
HOK TỐT
Cho ΔABCΔABC có A 60 độ , C 40 độ . Lấy điểm D trên cạnh AC của tam giác sao cho BDC 120 . Qua D kẻ đường thẳng song song với BC , cắt AB tại E
a) Tính BED và BDE
b) phân giác của góc BDF cắt BC ở F . CHứng minh rằng DF//AB
c) Chứng minh rằng DFBE
d) chứng minh rằng 2 đoạn thẳng BD Và EF cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó
Đọc tiếp
Cho có A = 60 độ , C =40 độ . Lấy điểm D trên cạnh AC của tam giác sao cho BDC = 120 . Qua D kẻ đường thẳng song song với BC , cắt AB tại E
a) Tính BED và BDE
b) phân giác của góc BDF cắt BC ở F . CHứng minh rằng DF//AB
c) Chứng minh rằng DF=BE
d) chứng minh rằng 2 đoạn thẳng BD Và EF cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó
Cho hình vẽ trong đó ADF90 đô ,DC là tia phân giác góc ADF. Hỏi AB, CD, EF, có song song với nhau không ? Vì sao ? A B D C E F 45 độ 135 độ
Đọc tiếp
Cho hình vẽ trong đó ADF=90 đô ,DC là tia phân giác góc ADF. Hỏi AB, CD, EF, có song song với nhau không ? Vì sao ?
Cho hình bình hành ABCD, chia hình bình hành thành 2 tam giác bằng nhau: tam giác ADC=tam giác BCA. Chứng minh AB song song với CD, AD song song với BC biết góc D=120 độ.
Cho hình bình hành ABCD, chia hình bình hành thành 2 tam giác bằng nhau: tam giác ADC=tam giác BCA. Chứng minh AB song song với CD, AD song song với BC biết góc D=120 độ.
hình bình hành ABCD vốn dĩ đã có AB//CD và AD//BC rồi nên không cần chứng minh đâu
tick đúng nha
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có ∠A = ∠D = 90 độ và AB = 1/2 CD. Kẻ DH vuông với AC, gọi M và N lần lượt là trung điểm của HD và HC
a) Chứng minh MN song song và bằng AB. Từ đó chứng minh MN vuông với AD tại E
b) Chứng minh AM vuông với DN
c) Chứng minh ∠BND = 90 độ
a, MN là đường trung bìng của tam giác HDC nên MN =1/2 CD và MN song song với CD
Mà AB song song với CD và AB=1/2 CD
Do đó: MN song song với AB và MN = AB (1)
MN song song với AB và AB vuông góc với AD nên MN vuông góc với AD tại E
b, Bạn chứng minh được M là trực tâm của tam giác ADN
Vì thế AM vuông góc với DN. (2)
c, TỪ (1) suy ra: AMNB là hình bình hành.
Nên AM song song với BN (3)
Từ (2) và (3) ,ta có: BN vuông góc với DN
Vậy góc BND = 90 độ.
Bài này bình thường ấy mà. Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD). Các đường phân giác ngoài của
A
^
và
D
^
cắt nhau tại E, các đường phân giác ngoài của
B
^
và
C
^
cắt nhau tại F. Chứng minh:a) EF song song với AB và CD;b) EF có độ dài bằng nửa chu vi hình thang ABCD
Đọc tiếp
Cho hình thang ABCD (AB//CD). Các đường phân giác ngoài của A ^ và D ^ cắt nhau tại E, các đường phân giác ngoài của B ^ và C ^ cắt nhau tại F. Chứng minh:
a) EF song song với AB và CD;
b) EF có độ dài bằng nửa chu vi hình thang ABCD
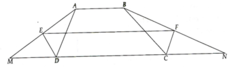
a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )
Lưu ý: Có thể sử dụng tính chất đường phân giác để chứng minh
Đúng 0
Bình luận (0)




