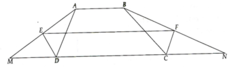
a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )
Lưu ý: Có thể sử dụng tính chất đường phân giác để chứng minh




