Cho x,y,z thỏa mãn x+y+2z=3.Tìm GTNN của biểu thức Q=2x2 - 2y2 - z2
QD
Những câu hỏi liên quan
cho các số dương x,y,z thỏa mãn x+y+z=1 tìm min của biểu thức
P=√(2x2+xy+2y2) +√(2y2+yz+2z2)+ √(2z2+xz+2x2)
Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737
Đúng 1
Bình luận (0)
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
Cho x,y,z là các số thực dương thỏa mãn điều kiện x+y+z=1. Tìm GTNN của biểu thức \(A=\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+1}\)
Cho x,y,z lớn hơn 0 thỏa mãn 13x+5y+12z=9. Tìm GTLN của biểu thức \(B=\frac{xy}{2x+y}+\frac{3yz}{2y+z}+\frac{6zx}{2z+x}\)
Giúp mk nhanh nhé mọi người ơi
\(A=\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+1}\).Áp dụng BĐT Cauchy-Schwarz,ta có:
\(=\left(1-\frac{1}{x+1}\right)+\left(1-\frac{1}{y+1}\right)+\left(1-\frac{1}{z+1}\right)\)
\(=\left(1+1+1\right)-\left(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}\right)\)
\(\ge3-\frac{9}{\left(x+y+z\right)+\left(1+1+1\right)}=\frac{3}{4}\)
Dấu "=" xảy ra khi x = y = z = 1/3
Vậy A min = 3/4 khi x=y=z=1/3
Đúng 0
Bình luận (0)
Bỏ chữ "Áp dụng bđt Cauchy-Schwarz,ta có:"giùm mình,nãy đánh nhầm ở bài làm trước mà quên xóa đi!
Đúng 0
Bình luận (0)
À mà để phải là tìm Max mới đúng chứ nhỉ?
Do đó,bạn sửa dòng: \(\ge3-\frac{9}{\left(x+y+z\right)+\left(1+1+1\right)}=\frac{3}{4}\) đến hết thành:
"\(\le3-\frac{9}{\left(x+y+z\right)+\left(1+1+1\right)}=\frac{3}{4}\)
Dấu "=" xảy ra khi x=y=z=1/3
Vậy A max = 3/4 khi x=y=z=1/3
Đúng 0
Bình luận (0)
Cho x,y,z là các số thực dương thỏa mãn điều kiện x+y+z=1. Tìm GTNN của biểu thức \(A=\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
Cho x,y,z lớn hơn 0 thỏa mãn 13x+5y+12z=9. Tìm GTLN của biểu thức \(b=\dfrac{xy}{2x+y}+\dfrac{3yz}{2y+z}+\dfrac{6zx}{2z+x}\)
Giúp mk nhanh nhé mọi người ơi
Cho hai số thực dương x,y thỏa mãn 2x + 2y 4. Tìm giá trị lớn nhất Pmax của biểu thức P (2x2 + y)(2y2 + x) + 9xy. A. Pmax
27
2
B. Pmax 18 C. Pmax 27 D. Pmax 12
Đọc tiếp
Cho hai số thực dương x,y thỏa mãn 2x + 2y = 4. Tìm giá trị lớn nhất Pmax của biểu thức
P = (2x2 + y)(2y2 + x) + 9xy.
A. Pmax = 27 2
B. Pmax = 18
C. Pmax = 27
D. Pmax = 12
Đáp án B.
Ta có 4 = 2 x + 2 y ≥ 2 2 x . 2 y = 2 2 x + y
⇔ 4 ≥ 2 x + y ⇔ x + y ≤ 2 .
Suy ra x y ≤ x + y 2 2 = 1
Khi đó
P = 2 x 3 + y 3 + 4 x 2 y 2 + 10 x y 2 x + y x + y 2 - 3 x y + 2 x y 2 + 10 x y
≤ 4 4 - 3 x y + 4 x 2 y 2 + 10 x y
= 16 + 2 x 2 y 2 + 2 x y x y - 1 ≤ 18
Vậy Pmax = 18 khi x = y = 1.
Đúng 0
Bình luận (0)
Cho hai số dương x,y thỏa mãn: 2x3-2x2+x2y+2xy2+y3-2y2=0
Tìm giá trị nhỏ nhất của biểu thức Q=\(\dfrac{3}{9x^2+6xy+y^2}=\dfrac{3}{3x^2+6xy+2y^2}\)
Chắc đề bài là \(Q=\dfrac{3}{9x^2+6xy+y^2}+\dfrac{3}{3x^2+6xy+2y^2}\)
Từ giả thiết ta có:
\(2x^3+2xy^2+xy^2+y^3=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x\left(x^2+y^2\right)+y\left(x^2+y^2\right)=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x+y=2\)
Do đó:
\(Q=3\left(\dfrac{1}{9x^2+6xy+y^2}+\dfrac{1}{3x^2+6xy+2y^2}\right)\)
\(Q\ge\dfrac{3.4}{12x^2+12xy+3y^2}=\dfrac{4}{\left(2x+y\right)^2}=1\)
\(Q_{min}=1\) khi \(\left\{{}\begin{matrix}2x+y=2\\9x^2+6xy+y^2=3x^2+6xy+2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{6}-2\\y=6-2\sqrt{6}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho các só thực x, y, z thỏa mãn điều kiện
x
-
y
+
z
3
x
2
+
y
2
+...
Đọc tiếp
Cho các só thực x, y, z thỏa mãn điều kiện x - y + z = 3 x 2 + y 2 + z 2 = 5 . Hỏi biểu thức P = x + y - 2 z + 2 có thể nhận bao nhiêu giá trị nguyên?
A. 2
B. 1
C. 3
D. 4
Chọn đáp án A
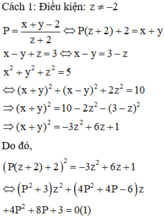

Do đó, P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Trong biểu thức P vai trò của z khác x, y do đó, ta tìm cách rút x, y theo z từ điều kiện ban đầu. Từ đó quy về phương trình ẩn z và tìm điều kiện để phương trình có nghiệm |

Phương trình (2), (3) là các phương trình mặt phẳng
Hai mặt phẳng này cắt nhau theo giao tuyến d có vecto chỉ phương là

Phương trình (4) là phương trình mặt cầu (S) có tâm O(0;0;0) bán kính R = 5
X, y, z tồn tại khi và chỉ khi d cắt (S)

Do đó P có thể nhận các giá trị nguyên là 0; -1
STUDY TIP |
Các biểu thức liên hệ giữa x, y, z có dạng phương trình mặt phẳng, mặt cầu. Từ đó giúp ta nghĩ đến việc xét vị trí tương dối giữa mặt cầu, với đường thẳng và mặt phẳng |
Đúng 0
Bình luận (0)
Cho 3 số dương x,y,z thỏa mãn x+y+z=2. tìm GTNN của biểu thức : P = \(\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\)
\(P\ge\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=1.\)
Dấu "=" xảy ra khi:
\(x=y=z=\frac{2}{3}\)
Đúng 0
Bình luận (0)
Áp dụng BĐT Cô-si cho 2 số dương \(\frac{x^2}{y+z}\)và \(\frac{y+z}{4}\), ta được :
\(\frac{x^2}{y+z}+\frac{y+z}{4}\ge2\sqrt{\frac{x^2}{y+z}.\frac{y+z}{4}}=2.\frac{x}{2}=x\) ( 1 )
Tương tự : \(\frac{y^2}{x+z}+\frac{x+z}{4}\ge y\) ( 2 )
\(\frac{z^2}{x+y}+\frac{x+y}{4}\ge z\) ( 3 )
Cộng ( 1 ) , ( 2 ) và ( 3 ) , ta được :
\(\left(\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\right)+\frac{x+y+z}{2}\ge x+y+z\)
\(P\ge\left(x+y+z\right)-\frac{x+y+z}{2}=1\)
Dấu " = " xảy ra \(\Leftrightarrow\)x = y = z = \(\frac{2}{3}\)
Vậy GTNN của P là 1 \(\Leftrightarrow\)x = y = z = \(\frac{2}{3}\)
Đúng 0
Bình luận (0)
\(\frac{x^2}{y+z}+x+\frac{y^2}{x+z}+y+\frac{z^2}{x+y}+z=\frac{x\left(x+y+z\right)}{y+z}+\frac{y\left(x+y+z\right)}{x+z}+\frac{z\left(x+y+z\right)}{x+y}\)
\(\Rightarrow P+\left(x+y+z\right)=\left(x+y+z\right)\left(\frac{x}{x+y}+\frac{y}{x+z}+\frac{z}{x+y}\right)\)hay \(P+2=2\cdot\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\right)\).Mặt khác \(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}=\frac{x^2}{xy+xz}+\frac{y^2}{yz+yx}+\frac{z^2}{zx+zy}\ge\frac{\left(x+y+z\right)^2}{2\left(xy+yz+zx\right)}\ge\frac{3\left(xy+yz+zx\right)}{2\left(xy+yz+zx\right)}=\frac{3}{2}\)
Do đó \(P+2\ge2\cdot\frac{3}{2}=3\Rightarrow P\ge1\)
Dấu '=' xảy ra khi \(\hept{\begin{cases}\frac{x}{xy+xz}=\frac{y}{yx+yz}=\frac{z}{zx+zy}\\x=y=z\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{1}{y+z}=\frac{1}{x+z}=\frac{1}{x+y}\\x=y=z\end{cases}\Leftrightarrow}x=y=z=\frac{2}{3}}\)
Xem thêm câu trả lời



