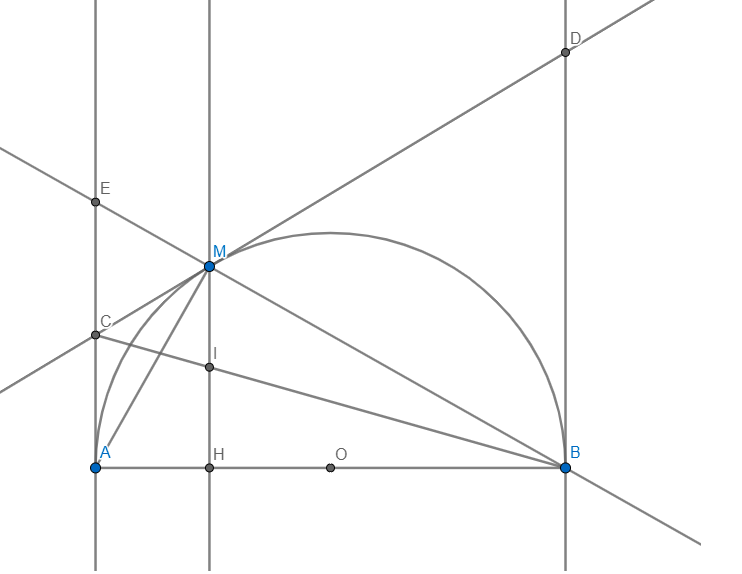
cho nửa đường tròn tâm O đường kính AB , tiếp tuyến Ax và By . Gọi C là điểm nằm giữa A và B ; M là một điểm nằm trên nửa đường tròn . Qua M kẻ đường thẳng vuông góc với CM cắt Ax ở D và cắt By ở E .
a , ACMD , BCME là tứ giác nội tiếp đường tròn
b, so sánh góc MDC với góc MAB và góc MEC với góc MBA
c, chứng minh tam giác CDE vuông