Viết phương trình đường thẳng Δ⊥d:\(\dfrac{x-1}{3}=\dfrac{y-2}{4}\).
biết d(M,Δ)=3 với M(2;-5)
giúp mình với bài này mình chưa làm được
cảm ơn
Cho đường thẳng Δ có phương trình \(\left\{{}\begin{matrix}x=5t\\y=-1+6t\\z=2\end{matrix}\right.\) và mặt phẳng 2x-y-4z+3=0. Hình chiếu vuông góc d' của Δ lên mặt phẳng (P) theo phương d: \(\dfrac{x-1}{2}=\dfrac{y}{4}=\dfrac{z+3}{-1}\)
Đường thẳng Δ có phương trình tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=-3-t\end{matrix}\right.\) và 2 điểm M(2;3), N(4;2)
Viết phương trình đường thẳng d' đi qua O biết (Δ,d')=450
Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
Lập phương trình thanh số, phương trình tổng quát của đường thẳng Δ biết: d. Δ đi qua D(2; 5) và E(3; 1)
e. Δ đi qua G(2; 5) và song song với đường thẳng d: 2x-3y-3 = 0
g. Δ đi qua H(2; 5) và vuông góc với đường thẳng d: x + 3y + 2 = 0
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
A nhé
hihhihihiihihihhiihhiihihihih
Trong mặt phẳng Oxy,cho hai điểm A(2;5); B(5;1) và đường thẳng (Δ):3x+4y-1=0
a)Viết phương trình đường thẳng đi qua hai điểm A,B
b)Viết phương trình đường thẳng (D) vuông góc với đường thẳng (Δ) và (D) cách điểm B một khoảng băng \(\dfrac{1}{5}\)
a.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình AB:
\(4\left(x-2\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-23=0\)b.
Do d vuông góc delta nên d nhận (4;-3) là 1 vtpt
Phương trình d có dạng: \(4x-3y+c=0\)
\(d\left(B;d\right)=\dfrac{\left|4.5-3.1+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{1}{5}\)
\(\Rightarrow\left|c+17\right|=1\Rightarrow\left[{}\begin{matrix}c=-16\\c=-18\end{matrix}\right.\)
Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x-3y-16=0\\4x-3y-18=0\end{matrix}\right.\)
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:
a, d: 2x-y+1=0, Δ: 3x-4y+2=0
b, d: x-2y+4=0, Δ: 2x+y-2=0
c, d: x+y-1=0, Δ: x-3y+3=0
d, d: 2x-3y+1=0, Δ: 2x-3y-1=0
Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:
a, d: 2x-y+1=0, I(2;1)
b, d: x-2y+4=0, I(-3;0)
c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
mỗi bài, mk làm một phần ví dụ cho cậu nhé
nó đối xứng với nhau qua pt đường thẳng đenta,
trường hợp (d) ko cắt (đen ta) hay (d) cắt (đen ta) thì đều làm theo phương pháp sau
lấy 2 điểm bất kì thuộc (d) thì ta có như sau: A(0:1) là điểm thuộc đường thẳng (d)
lấy A' đối xứng với A qua (đen ta)
liên hệ tính chất đối xứng qua đường thẳng thì hiểu là AA' vuông góc (đen ta)
đồng thời giao điểm của AA' với (đen ta) là trung điểm của AA'
dễ dàng tìm đc giao điểm của (đen ta) với (d) là K(-2/5;1/5)
từ pt (đenta) thì dễ dàng =) vecto pháp tuyến của (đenta) =) (3;-4)
vì AA' vuông góc với (đenta) nên =) vectơ pháp tuyến của AA' là (4;-3)
áp véctơ pháp tuyến của AA' vào phương trình tổng quát đc: 4(x-0)-3(y-1)=0 (=) 4x-3y+3=0
gọi I là giao điểm của AA' và (đenta) =) I(-6/7;-1/7)
mà I là trung điểm của AA'
chắc chắn cậu sẽ dễ dàng suy ra điểm A'
mà K và A' thuộc (d') nên dễ dàng =) phương trình của (d')
cho đường thẳng y=mx+n(Δ).Tìm m và n để đường thẳng (Δ) // với đường thẳng y=-2x+5(d) và có duy nhất 1 điểm chung với đồ thị (P)y=\(\dfrac{-1}{2}\)x2
Vì (Δ) // (d) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n\ne5\end{matrix}\right.\) \(\Rightarrow\left(\Delta\right):y=-2x+n\)
Phương trình hoành độ giao điểm của (Δ) và (P)
\(-2x+n=-\dfrac{1}{2}x^2\) \(\Leftrightarrow\dfrac{1}{2}x^2-2x+n=0\) (*)
Ta có: \(\Delta'=1-\dfrac{1}{2}n\)
Để (Δ) và (P) có 1 điểm chung duy nhất
\(\Leftrightarrow\) Phương trình (*) có nghiệm kép \(\Leftrightarrow1-\dfrac{1}{2}n=0\) \(\Leftrightarrow n=2\) (Thỏa mãn)
Vậy \(m=-2\) và \(n=2\)
Trong không gian Oxyz, cho đường thẳng d: x = 1 + t, y = 2 -2t, z = -3. Viết phương trình tham số của đường thẳng Δ nằm trong mặt phẳng (Oxy), song song với d sao cho khoảng cách giữa hai đường thẳng d và Δ đạt giá trị nhỏ nhất
A. d: x = 1 + t, y = 2 -2t, z = 0
B. d: x = 1 + t, y = -2t, z = -3
C. d: x = t, y = 2 - 2t, z = -3
D. d: x = 1, y = 2, z = -3 + t
Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 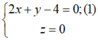
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 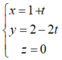
Lập phương trình đường thẳng y= ax + b,biế
1. Δ đi qua điểm A(3;-2) và B(2;1)
2. Δ đi qua điểm E(3;3) và song song với đường thẳng d : y=-3x+2 3. ΔΔ đi qua điểm G(1;1) và vuông góc với đường thẳng d: y=-x+1
1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6