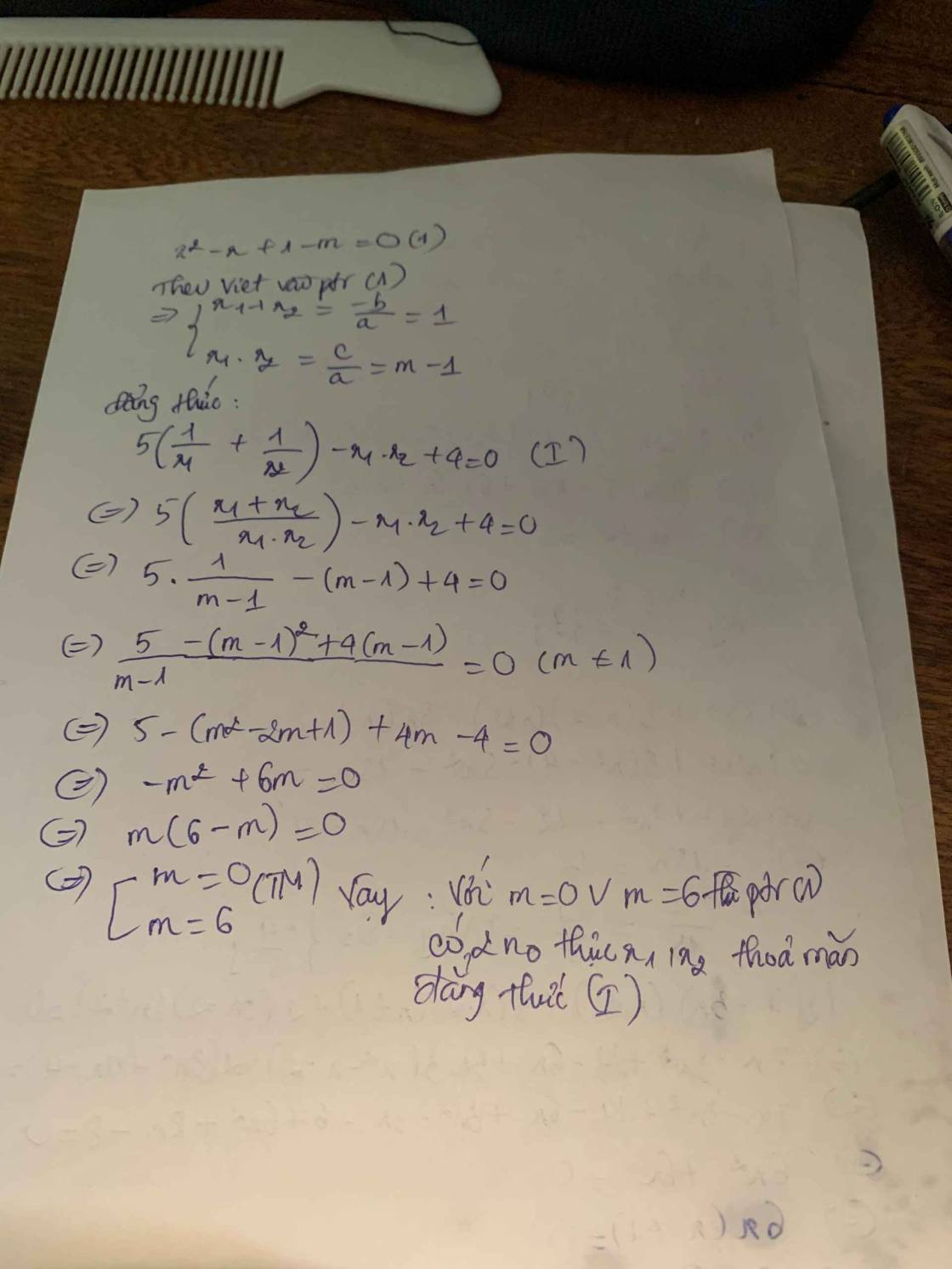để pt trên vô nghiệm thì x sẽ bằng -1 

\(\dfrac{x\left(x+n\right)}{x\left(x+1\right)}+\dfrac{\left(x-2\right)\left(x+1\right)}{x\left(x+1\right)}-\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}=0\)

\(x^2+xn+x^2+x-2x-2-2x^2-2x=0\)

thay x = -1 để tìm n:

\(\left(-1\right)^2-n+\left(-1\right)^2-1-2.\left(-1\right)-2-2.\left(-1\right)^2-2.\left(-1\right)=0\)

\(1-n+1-1=0\)

\(1-n=0\)

=> n = 1 thì pt vô nghiệm.

Yên tâm cj thay n= 1 vô tìm x giải ra x = -1(ktm) pt vô nghiệm r.

Nó lớp 2 thiệt hả bn

mất niềm tin về cuộc sống

`2/(x+1)-m/(x-2)=0(x\ne-1,x\ne2)`

`<=>2/(x+1)=m/(x-2)`

`<=>2(x-2)=m(x+1)`

`<=>2x-4=mx+m`

`<=>mx-2x=-m-4`

`<=>x(m-2)=-4-m`

Để pt có nghiệm

`=>m-2ne0=>m ne 2`

`=>x=(-4-m)/(m-2)`

`x ne -1=>(-4-m)/(m-2)\ne-1`

`=>(-m-4)/(m-2)+1\ne0`

`<=>-2/(m-2) ne 0` luôn đúng với m khác 2

`x ne 2=>(-4-m)/(m-2)\ne2`

`=>(-m-4)/(m-2)-2 \ne 0`

`=>(-3m-8)/(m-2)\ne0`

`=>-3m-8\ne0`

`=>m\ne-8/3`

Vậy với `m ne 2` và `m ne -8/3` thì pt có nghiệm

Đk: \(\left\{{}\begin{matrix}x+1\ne0\\x-2\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne2\end{matrix}\right.\)

Pt: \(\Rightarrow2\left(x-2\right)-m\left(x+1\right)=0\)

     \(\Rightarrow2x-4-mx-m=0\) \(\Rightarrow x\left(2-m\right)=m+4\)

     \(\Rightarrow x=\dfrac{m+4}{2-m}\)

Mà \(x\ne-1vàx\ne2\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{m+4}{2-m}\ne-1\\\dfrac{m+4}{2-m}\ne2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4\ne-2\left(luônđúng\right)\\m\ne0\end{matrix}\right.\)

Vậy với \(m\ne0\) thì pt có nghiệm.

\(\dfrac{x+1}{x+2}=\dfrac{x-1}{x-m}\)

\(\Leftrightarrow\left(x+1\right)\left(x-m\right)=\left(x+2\right)\left(x-1\right)\)

\(\Leftrightarrow x^2-xm+x-m=x^2+x-2\)

\(\Leftrightarrow-xm+2=0\)

Để pt vô nghiệm thì \(a\ne0\) nhưng trong TH này \(a=0\)

Vậy m không xác định

PT \(\Leftrightarrow\dfrac{m\left(1-mx\right)+1+mx}{\left(1+mx\right)\left(1-mx\right)}=\dfrac{1}{\left(1-mx\right)\left(1+mx\right)}\)

\(\Rightarrow m-m^2x+1+mx=1\)

\(\Leftrightarrow x\left(m-m^2\right)+m=0\)

Để phương trình vô nghiệm  \(\Leftrightarrow\left\{{}\begin{matrix}m-m^2=0\\m\ne0\end{matrix}\right.\)

\(\Leftrightarrow m=1\)
Vậy \(m=1\)

\(x^2-x+1-m=0\)

Theo Vi - ét, ta có :

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=1-m\end{matrix}\right.\)

Ta có :

\(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)

\(\Leftrightarrow5\left(\dfrac{x_2+x_1}{x_1x_2}\right)-x_1x_2+4=0\)

\(\Leftrightarrow5\left(\dfrac{1}{1-m}\right)-\left(1-m\right)+4=0\)

\(\Leftrightarrow\dfrac{5}{1-m}-1+m+4=0\)

\(\Leftrightarrow\dfrac{5}{1-m}+m+3=0\)

\(\Leftrightarrow\dfrac{5+m\left(1-m\right)+3\left(1-m\right)}{1-m}=0\)

\(\Leftrightarrow5+m-m^2+3-3m=0\)

\(\Leftrightarrow-m^2-2m+8=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)

Bước 1: Tìm điều kiện của tham số để phương trình có hai nghiệm phân biệt.

Bước 2: Khi phương trình đã có hai nghiệm phân biệt, ta áp dụng Vi-ét để tìm các giá trị của tham số.

Bước 3. Đối chiếu với điều kiện và kết luận bài toán.

xem tr sách của anh

Bài 1:

PT có 2 nghiệm \(\Leftrightarrow\Delta=\left(m+2\right)^2-4\cdot2\ge0\Leftrightarrow m^2+4m-8\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2-2\sqrt{3}\\m\ge-2+2\sqrt{3}\end{matrix}\right.\)

Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=2\end{matrix}\right.\)

Ta có \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{9}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=9x_1x_2\)

\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=18\\ \Leftrightarrow2\left(m+2\right)^2-8=18\\ \Leftrightarrow2m^2+8m+8-8=18\\ \Leftrightarrow m^2+4m-9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2+\sqrt{13}\\m=-2-\sqrt{13}\end{matrix}\right.\left(tm\right)\)

ĐKXĐ: \(x>1\)

- Với \(m=0\) thỏa mãn

- Với \(m\ne0\)

\(\Rightarrow m^2\left(x-1\right)+m=x\)

\(\Leftrightarrow\left(m^2-1\right)x=m^2-m\) (1)

Pt đã cho vô nghiệm khi:

TH1: (1) vô nghiệm \(\Leftrightarrow\) \(\left\{{}\begin{matrix}m^2-1=0\\m^2-m\ne0\end{matrix}\right.\) \(\Leftrightarrow m=-1\)

TH2: (1) có nghiệm thỏa mãn \(x\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\x=\dfrac{m^2-m}{m^2-1}\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\\dfrac{m}{m+1}-1\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\\dfrac{1}{m+1}\ge0\end{matrix}\right.\) \(\Leftrightarrow m>-1\)

Vậy pt vô nghiệm khi \(m\ge-1\)

A) delta=(4m-2)^2-4×4m^2

=16m^2-8m+4-16m^2

=-8m+4

để pt có hai nghiệm pb thì -8m+4>0

Hay m<1/2

B để ptvn thì -8m+4<0

hay m>1/2