Cho hình thang ABCD(AB//CD), có AB=7cm, CD=12cm; M trung điểm của CD, BD cắt AM tại E, AC cắt BM tại F
a) chứng minh EF//AB
b) tính EF
NL
Những câu hỏi liên quan
VP
20 tháng 4 2021 lúc 8:43
cho hình thang ABCD (AB//CD) có AB =7cm , CD=18cm hai đường chéo AC=20cm và BD=12cm. Từ A vẽ đường thẳng song song với BD, cắt CD tại E.
a/cm ABDE là hbh
b/ Chứng minh tam giác ACE là tam giác vuông?
c/ Tính diện tích hình thang ABCD
Cho hình thang ABCD, AB//CD, AB=7cm; CD=12cm. M là trung điểm của CD, BD cắt AM tại E; AC cắt BM tại F. Chứng minh :
a) EF//AB
b) EF =...cm?
Cho hình thang ABCD ,AB//CD,AD⊥AC.Biết AB\(=\)7cm ,CD\(=\)25cm.Tính diện tích hình thang
Cho hình thang ABCD(AB//CD) có AB = 7cm, CD=12cm. Gọi M là trung điểm của CD, E là gia điểm của MA và BD, F là giao điiểm của MB và AC.
a, chứng minh EF // với AB
b, tính độ dài đoạn EF
BFFM=ABCM(1)" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">AEEM=ABDM(2)" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">ABDM=ABMC(3)" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">AEEM=BFFM" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">AEEM=BFFM" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">MEAM=DMAB" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">EFAB=MEAM" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">DMAB=ÈFAB⇒EF=DM=122=6cm" role="presentation" tabindex="0" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; font-size:16px; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; text-align:left; white-space:nowrap; word-spacing:normal">DM/AB=EF/AB⇒EF=DM=12/2=6cm
Cho hình thang abcd (ab//cd) ab=7cm,cd=11cm .Tính độ dài đường trung bình của hình thang
Độ dài đường trung bình hthang:
\(\dfrac{AB+CD}{2}=\dfrac{7+11}{2}=\dfrac{18}{2}=9\left(cm\right)\)
Đúng 1
Bình luận (0)
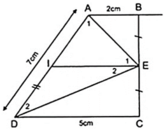
Cho hình thang ABCD ( AB//CD ) có AB = 2cm,CD = 5cm,AD = 7cm. Gọi E là trung điểm của BC. Tính A E D ^ = ?
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có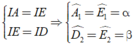
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có
Đúng 0
Bình luận (0)
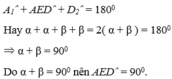
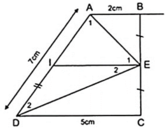
Cho hình thang ABCD ( AB//CD ) có AB = 2cm, CD = 5cm, AD = 7cm. Gọi E là trung điểm của BC. Tính A E D ^ = ?
Do E là trung điểm của BC theo giả thiết vẽ I là trung điểm của AD thì
AI = ID = AD/2 = 3,5( cm ). ( 1 )
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có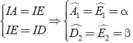
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có
Đúng 0
Bình luận (0)
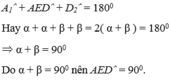
cho hình thang ABCD có AB//CD biết BD= 7cm , góc ABD = 45 độ. Tính diện tích hình thang ABCD
Gọi O là giao điểm của AC, BD, Kẻ BF ⊥ CD, Kẻ BE // AC
Xét ΔABD và ΔBAC có:
AD=BC (htc ABCD)
AB chung
góc DAB = góc ABC (htc ABCD)
⇒ △ABD=△BAC (c-g-c)
⇒ góc BAC = góc BAD = 45 độ
⇒ ΔOAB vuông cân tại O hay AC ⊥ BD ⇒ BE ⊥ BD ⇒ ΔBED vuông ở B
Tứ giác ABEC: BE // AC, AB // CE nên là hbh
⇒ BE = AC = BD = 7cm, AB = CE
ΔABD và ΔBCE có đường cao ứng với 2 đáy AB, CE bằng nhau cùng bằng BF, lại có AB = CE nên SABD = SBCE
⇒ SABCD = SBDE = 7.7/2 =
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD (AB song song với CD) có AB = 7cm, BC = CD= 13cm. Kẻ các đường cao AK và BH
a) Chứng minh rằng CH=DK và AB = HK
b) Tính độ dài BH và diện tích hình thang ABCD
a: Xét ΔAKD vuông tại K và ΔBHC vuông tại H có
AD=BC
góc D=góc C
=>ΔAKD=ΔBHC
=>CH=DK
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AB=HK
b: KH=AB=7cm
=>DK+HC=13-7=6cm
=>DK=HC=6/2=3cm
\(BH=\sqrt{13^2-3^2}=\sqrt{160}=4\sqrt{10}\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}\cdot BH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\sqrt{10}\left(7+13\right)=40\sqrt{10}\left(cm^2\right)\)
Đúng 1
Bình luận (0)