Làm rõ ràng hộ em ạ, cảm ơn ạ <3
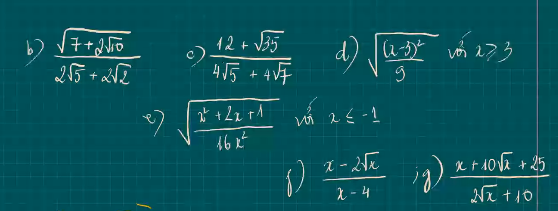
Làm rõ ràng hộ em ạ, em cảm ơn <3
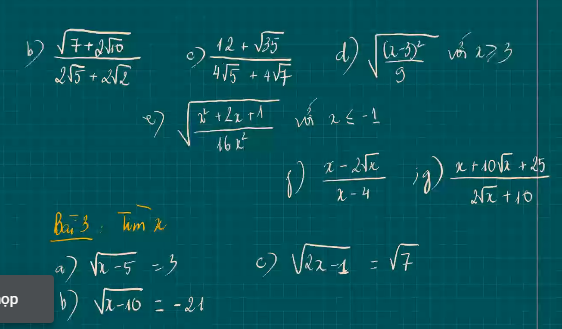
a) \(\sqrt{x-5}=3\)
\(x-5=9\)
\(x=14\)
b) Vì \(\sqrt{x-10}\) ≥0
⇒không có x thỏa mãn
c) \(\sqrt{2x-1}=\sqrt{7}\)
\(2x-1=7\)
\(2x=8\)
\(x=4\)
Bài 3
a) \(\sqrt{x-5}=3\)
\(\Rightarrow x-5=9\)
\(\Rightarrow x=14\)
b) \(\sqrt{x-10}=-21\)
\(\Rightarrow x\in\varnothing\)
c) \(\sqrt{2x-1}=\sqrt{7}\)
\(\Rightarrow2x-1=7\)
\(\Rightarrow2x=8\)
\(\Rightarrow x=4\)
Giải thích rõ ràng hộ em với (làm thành bài ạ). Em cảm ơn

Câu 12.
\(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{\dfrac{4a}{25}}\)
\(=5\sqrt{a}+6\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+5\dfrac{2\sqrt{a}}{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+2\sqrt{a}\) (vì a>0)
\(=8\sqrt{a}\)
Câu 13. Chọn C.
Do x,y\(\ge\)0, x\(\ne\)y ta có:
\(A=\dfrac{x-\sqrt{xy}}{x-y}=\dfrac{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\cdot\left(\sqrt{x}+\sqrt{y}\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
Nhờ mn giúp em với ạ, mn xem em làm bài đúng ko ạ?
Rút gọn:
\(\dfrac{x-2\sqrt{x}}{x-4}\)
Nhờ mọi người làm rõ ràng hộ em ạ, em cảm ơn <3
\(\dfrac{x-2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
Rút gon:
\(\sqrt{\dfrac{x^2+2x+1}{16x^2}}\) với \(x\) ≤ -1
Nhờ mọi người làm rõ ràng hộ em ạ, em cảm ơn <3
\(\sqrt{\dfrac{x^2+2x+1}{16x^2}}=\sqrt{\dfrac{\left(x+1\right)^2}{16x^2}}=\dfrac{\left|x+1\right|}{4\left|x\right|}=\dfrac{1-x}{-4x}=\dfrac{x-1}{4x}\left(do.x\le-1\right)\)
giúp mình với ạ mình cần cách làm rõ ràng ạ cảm ơn ạ!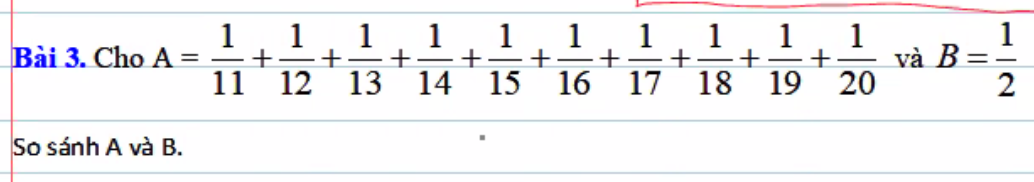
Tham khảo:
Ta có các phân số 1/11 ; 1/12 ; 1/13 ; 1/14 ; 1/15 ; 1/16 ; 1/17 ; 1/18 ; 1/19 đều lớn hơn 1/20
Do đó : 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16 + 1/17 + 1/18 + 1/19 + 1/20 > 1/20 + 1/20 + ;...+ 1/20 ( có 10 phân số 1/20 )
1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1 /16 + 1/17 + 1/18 + 1/19 + 1/20 > 10/20
1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1 /16 + 1/17 + 1/18 + 1/19 + 1/20 > 1/2
Vậy : S > 1/2
Ta có: \(\dfrac{1}{2}=\dfrac{10}{20}=\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\) ( Có 10 số \(\dfrac{1}{20}\) )
Mà \(\dfrac{1}{20}< \dfrac{1}{19}:\dfrac{1}{20}< \dfrac{1}{18}:...:\dfrac{1}{20}< \dfrac{1}{11}\)
\(\Rightarrow\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}< \dfrac{1}{20}+\dfrac{1}{19}+\dfrac{1}{18}+...+\dfrac{1}{11}\)
\(\Rightarrow A=B\)
Giúp mình với ạ làm rõ ràng giúp mình và nhanh ạ mình cảm ơn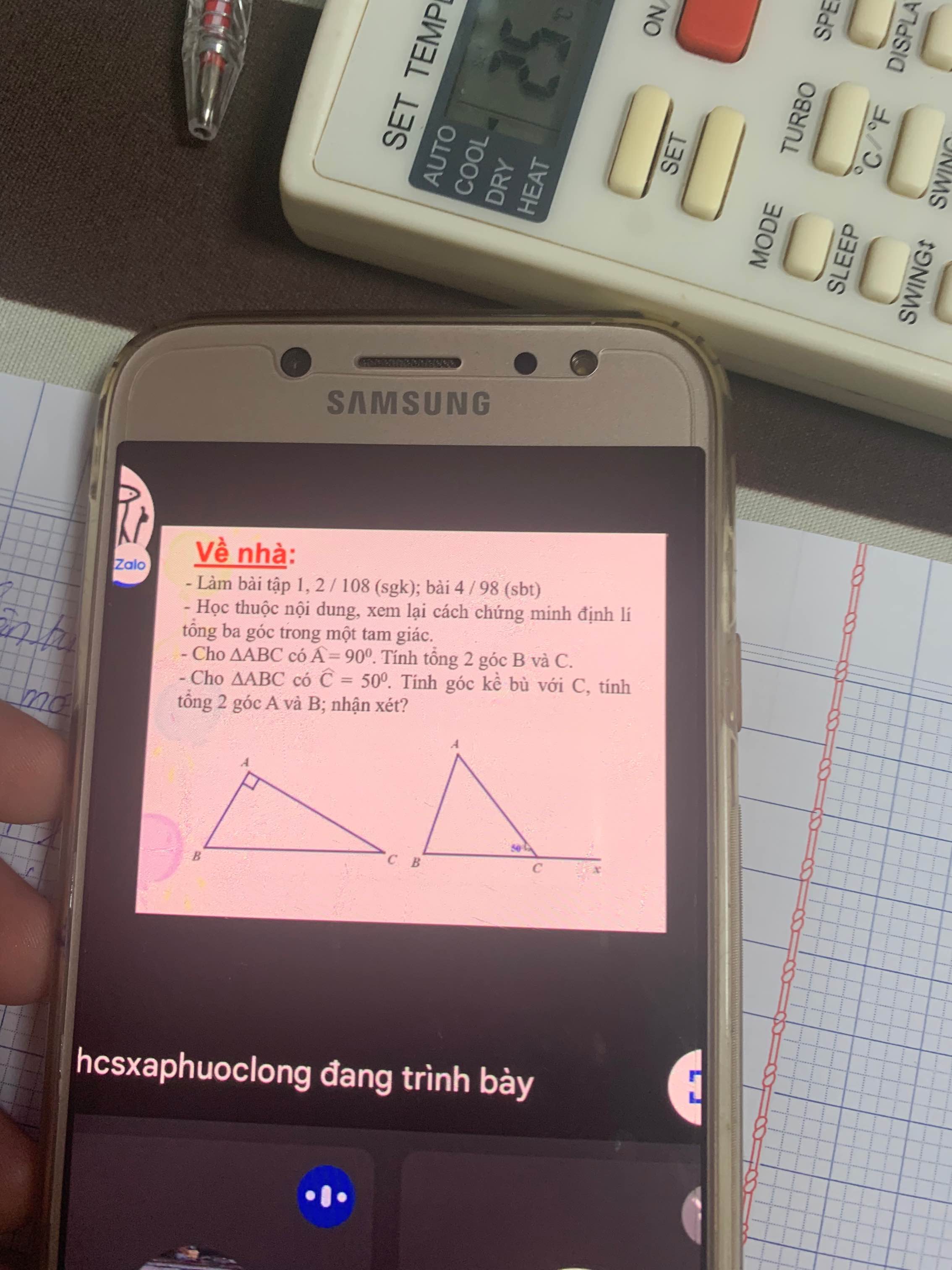
a: \(\widehat{B}+\widehat{C}=90^0\)
c: Góc kề bù với C bằng tổng của góc A cộng góc B
Tính bằng cách thuận tiện nhất :
89x 19 - 16 x 89 + 3 x 89
nhanh hộ em vs ạ
ghi rõ ràng ra giúp em nhé , em cảm ơn ^^
vâng ạ , em cảm ơn Phạm Thu Trang ạ <3

Mọi người giải giúp em với ạ, mai em thi rồi, mấy anh/chị giải thích rõ ràng giùm em nhé, em cảm ơn ạ.
Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)
17:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{3;1\right\}\)
=>\(x\in\left\{9;1\right\}\)
16:
a: BC=BH+CH
=9+16
=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>AM=AC/2=10(cm)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\dfrac{15}{10}=\dfrac{3}{2}\)
nên \(\widehat{AMB}\simeq56^0\)
GIẢI GIÚP EM CÂU 5 TRÌNH BÀY RÕ RÀNG DỄ HIẾU VỚI Ạ , EM CẢM ƠN 
Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật