Tìm các số nguyên tố cùng nhau trong các số sau: 6;35;21;143
PY
Những câu hỏi liên quan
Tìm các cặp số nguyên tố cùng nhau trong các số sau 3; 6; 7; 8; 15; 17;21; 23;24; 28; 29
1.Chứng minh rằng: Với mọi số tự nhiên các số sau là các số nguyên tố cùng nhau.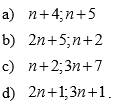
2.Tìm các số tự nhiên để các số sau nguyên tố cùng nhau. 
1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
Đúng 2
Bình luận (0)
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau
Đúng 1
Bình luận (0)
trong các số sau ,hai số nào là số nguyên tố cùng nhau??
tìm ƯCLN và BCNN của 2 số nguyên tố đó :12;15;25;30
Hai số nguyên tố cùng nhau:15;25
Ta có:
15=3*5
\(25=5^2\)
ƯCLN(15;25)=5
BCNN(25;15)=\(5^2\cdot3=75\)
Đúng 0
Bình luận (0)
Trong các số sau, hai số nào là hai số nguyên tố cùng nhau?
12;25;30;21
Ta có: 12 = 22.3
25 = 52
30 = 2.3.5
21 = 3.7
Suy ra: ƯCLN(12;25) = 1 và ƯCLN(25;21) =1
Vậy 12 và 25 là hai số nguyên tố cùng nhau.
25 và 21 là hai số nguyên tố cùng nhau.
Đúng 0
Bình luận (0)
Trong các số sau, hai số nào là hai số nguyên tố cùng nhau?
12;25;30;21.
Ta có: 12 = 22.3
25 = 52
30 = 2.3.5
21 = 3.7
Suy ra: ƯCLN(12;25) = 1 và ƯCLN(25;21) =1
Vậy 12 và 25 là hai số nguyên tố cùng nhau.
25 và 21 là hai số nguyên tố cùng nhau.
Hok tốt nha chủ tus chymte.
Đúng 0
Bình luận (0)
tìm các ƯC của các số sau ( 53;26;61;412;46;71;14) 7 số đó có phải là nguyên tố cùng nhau ko ?
có nguyên tố cùng nhau vì trong đó có các số nguyên tố
chúc bn hc tốt
mk lười tính lém sai thì thui
Tìm các số tự nhiên n để các số sau là nguyên tố cùng nhau 4n+3 và 2n+3
Cho các phát biểu sau: (1) Các nguyên tố nhóm A trong bảng tuần hoàn là các nguyên tố nhóm s (2) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong cùng một chu kì được lặp đi lặp lại sau mỗi chu kì (3) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong một nhóm A biến đổi một cách không tuần hoàn (4) Số thứ tự của nhóm (IA,IIA,..) cho biết số electron ở lớp ngoài cùng nhưng không cho biết số electron hóa trị trong nguyên tử của các nguyên tố đó (5) Nhóm VIIIA là...
Đọc tiếp
Cho các phát biểu sau:
(1) Các nguyên tố nhóm A trong bảng tuần hoàn là các nguyên tố nhóm s
(2) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong cùng một chu kì được lặp đi lặp lại sau mỗi chu kì
(3) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong một nhóm A biến đổi một cách không tuần hoàn
(4) Số thứ tự của nhóm (IA,IIA,..) cho biết số electron ở lớp ngoài cùng nhưng không cho biết số electron hóa trị trong nguyên tử của các nguyên tố đó
(5) Nhóm VIIIA là nhóm khí hiếm
(6) Nguyên tử của tất cả các nguyên tố trong nhóm khí hiếm đều có 8 electron ở lớp ngoài cùng
Số phát biểu đúng là:
A. 5
B. 2
C. 3
D. 4
Các trường hợp thỏa mãn: 1-5
ĐÁP ÁN B
Đúng 0
Bình luận (0)
Cho các phát biểu sau: (1) Các nguyên tố nhóm A trong bảng tuần hoàn là các nguyên tố nhóm s (2) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong cùng một chu kì được lặp đi lặp lại sau mỗi chu kì (3) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong một nhóm A biến đổi một cách không tuần hoàn (4) Số thứ tự của nhóm (IA, IIA,..) cho biết số electron ở lớp ngoài cùng nhưng không cho biết số electron hóa trị trong nguyên tử của các nguyên tố đó (5) Nhóm VIIIA là...
Đọc tiếp
Cho các phát biểu sau:
(1) Các nguyên tố nhóm A trong bảng tuần hoàn là các nguyên tố nhóm s
(2) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong cùng một chu kì được lặp đi lặp lại sau mỗi chu kì
(3) Cấu hình electron lớp ngoài cùng của nguyên tử các nguyên tố trong một nhóm A biến đổi một cách không tuần hoàn
(4) Số thứ tự của nhóm (IA, IIA,..) cho biết số electron ở lớp ngoài cùng nhưng không cho biết số electron hóa trị trong nguyên tử của các nguyên tố đó
(5) Nhóm VIIIA là nhóm khí hiếm
(6) Nguyên tử của tất cả các nguyên tố trong nhóm khí hiếm đều có 8 electron ở lớp ngoài cùng
Số phát biểu đúng là
A.5.
B. 2.
C. 3.
D. 4.


