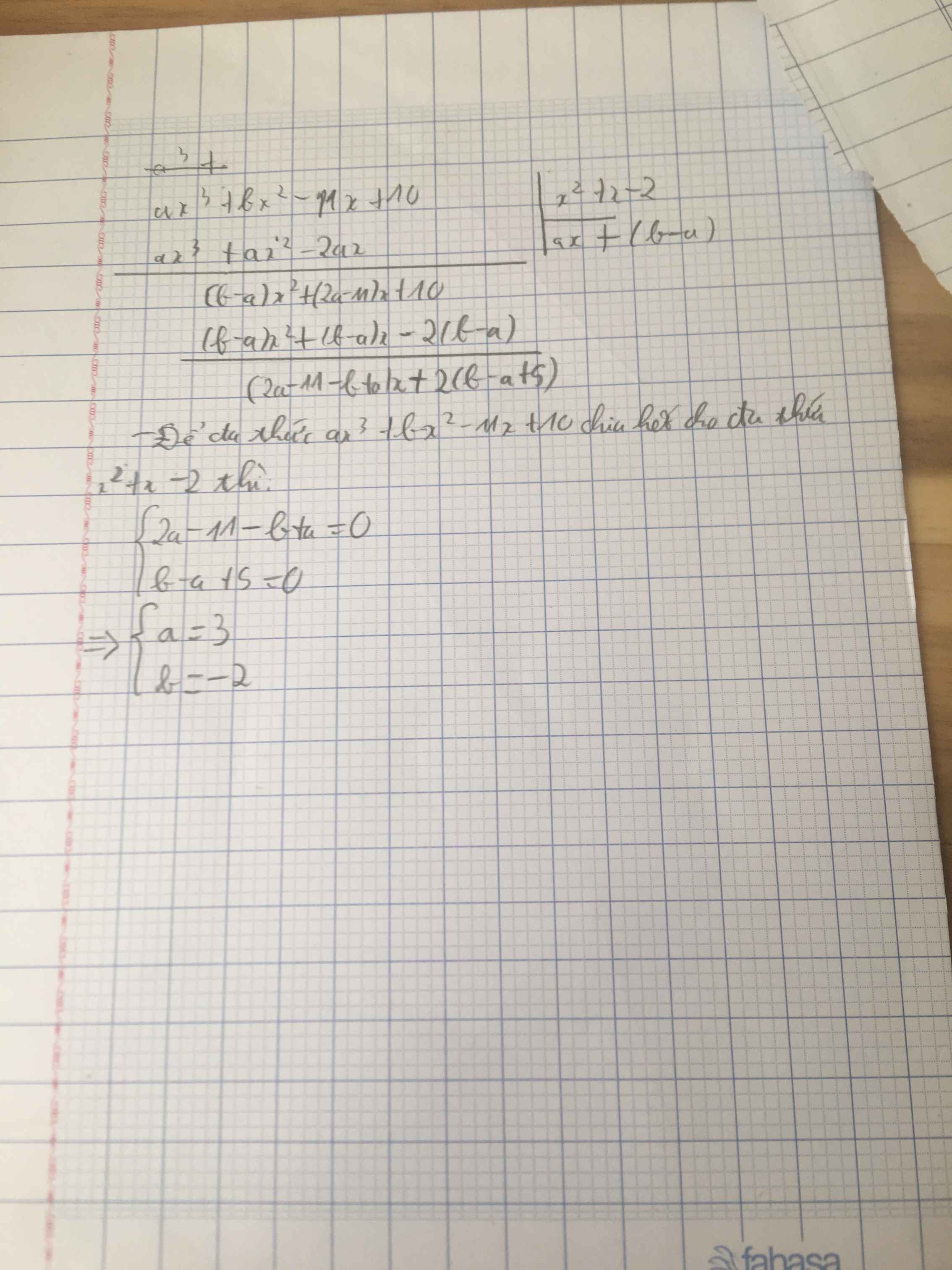xác định a,b để đa thức f(x)=2ax2+bx-3 chia hết cho 4x-1 và x+3
TN
Những câu hỏi liên quan
Cho đa thức F ( x ) = 2 a x 2 + b x (a,b là hằng số). Xác định a,b để đa thức F(x) có nghiệm x = - 1 v à F ( 1 ) = 4
Cho đa thức F(x) = 2ax2 + bx (a,b là hằng số). Xác định a,b để đa thức F(x) có nghiệm x = -1 và F(1) = 4
Vì đa thức F(x) có nghiệm x = -1 nên thay F(-1) = 0
⇒ 2a - b = 0 ⇒ b = 2a (0.5 điểm)
Vì F(1) = 4 ⇒ 2a + b = 4 ⇒ b = 4 - 2a
Từ đây ta có 2a = 4 - 2a ⇒ 4a = 4 ⇒ a = 1 (0.5 điểm)
Đúng 0
Bình luận (0)
Cho đa thức H ( x ) = 2 a x 2 + b x . Xác định a,b để đa thức H(x) có nghiệm là x = -1 và H(1) = 4
A. a = 2, b = 1
B. a = 1, b = 2
C. a = -1, b = -2
D. a = -2, b = -1
Vì x = -1 là nghiệm của H(x) nên
H(-1) = 0 ⇒ 2a(-1)2 + b(-1) = 2a - b = 0 ⇒ b = 2a
Vì H(1) = 4 ⇒ 2a.12 + b.1 = 2a + b = 4 ⇒ b = 4 - 2a
Ta có 2a = 4 - 2a ⇒ 4a = 4 ⇒ a = 1, từ đó b = 2. Chọn B
Đúng 0
Bình luận (0)
Cho đa thức F(x) = 2ax2 + bx
Xác định a;b để đa thức F(x) có nghiệm x= -1 và F(1) = 4
Thay x= - 1 vào đa thức , ta có
F(x)= 2a(-1)2 + b(-1)
F(x)= 2a-b
Đặt F(x)=0, ta có :
2a-b=0=> 2a = b hay b gấp đôi a
Đúng 0
Bình luận (2)
Bài 3. (1 điểm). Xác định a để đa thức f(x)=x^3 –4x^2 +6x− a chia hết cho đa thức g(x)=x-2
\(\Leftrightarrow x^3-2x^2-2x^2+4x+2x-4-a+4⋮x-2\)
hay a=4
Đúng 1
Bình luận (0)
xác định hệ số a b c sao cho đa thức f(x)= 2x^4+ax^2 +bx+c chia hết cho x-2 khi chia f(x) cho x^2-4x+3 thì được phần dư là -x+2
\(f\left(x\right)=2x^4+ax^2+bx+c\)
\(=2x^4-4x^3+4x^3-8x^2+\left(a+8\right)x^2-x\left(2a+16\right)+\left(2a+16+b\right)x-2\left(2a+16+b\right)+4a+32+2b+c\)
\(=\left(x-2\right)\left(2x^3+4x^2+x\left(a+8\right)+2a+16+b\right)+4a+2b+32+c\)
=>\(\dfrac{f\left(x\right)}{x-2}=2x^3+4x^2+x\left(a+8\right)+2a+16+b+\dfrac{4a+2b+32+c}{x-2}\)
f(x) chia hết cho x-2 nên \(4a+2b+32+c=0\)(1)
\(f\left(x\right)=2x^4+ax^2+bx+c\)
\(=2x^4-4x^3+6x^2+4x^3-16x^2+12x+\left(a+10\right)x^2-4x\left(a+10\right)+3a+30+x\left(4a+28+b\right)+c-3a-30\)
\(=\left(x^2-4x+3\right)\left(2x^2+4x+a+10\right)\)+x(4a+28+b)+c-3a-30
f(x) chia cho x2-4x+3 dư -x+2 nên ta có:
\(\left\{{}\begin{matrix}4a+28+b=-1\\c-3a-30=2\end{matrix}\right.\)(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+2b+32+c=0\\4a+b+28=-1\\c-3a=32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4a+2b+c=-32\\4a+b=-29\\-3a+c=32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b+c=-3\\-3a+c=32\\4a+b=-29\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+3a=-35\\4a+b=-29\\b+c=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-a=-6\\4a+b=-29\\b+c=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=-29-4a=-29-4\cdot6=-53\\c=-3-b=-3-\left(-53\right)=50\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1)cho f(x)ax^3+bx^2+cx+d trong đó a,b,c,d thuộc Z và thỏa mãn b3a+c.Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.2)cho đa thức f(x)ax^2+bx+c với a,b,c là hằng số.Hãy xác định a,b,c biết f(1)4,f(-1)8 và a-c43)cho f(x)ax^3+4x(x^2-1)+8;g(x)x^3-4x(bx-1)+c-3.Xác định a,b,c để f(x)g(x).4)cho f(x)cx^2+bx+a và g(x)ax^2+bx+c.cmr nếu Xo là nghiệm của f(x) thì 1/Xo là nghiệm của g(x)5)cho đa thức f(x) thỏa mãn xf(x+2)(x^2-9)f(x).cmr đa thức f(x) có ít nhất 3 nghiệm6)tính f(2) biết f(x)+(x+1)...
Đọc tiếp
1)cho f(x)=ax^3+bx^2+cx+d trong đó a,b,c,d thuộc Z và thỏa mãn b=3a+c.Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.
2)cho đa thức f(x)=ax^2+bx+c với a,b,c là hằng số.Hãy xác định a,b,c biết f(1)=4,f(-1)=8 và a-c=4
3)cho f(x)=ax^3+4x(x^2-1)+8;g(x)=x^3-4x(bx-1)+c-3.Xác định a,b,c để f(x)=g(x).
4)cho f(x)=cx^2+bx+a và g(x)=ax^2+bx+c.
cmr nếu Xo là nghiệm của f(x) thì 1/Xo là nghiệm của g(x)
5)cho đa thức f(x) thỏa mãn xf(x+2)=(x^2-9)f(x).cmr đa thức f(x) có ít nhất 3 nghiệm
6)tính f(2) biết f(x)+(x+1)f(-x)=x+2
Xác định hệ số a,b sao cho đa thức :
f(x)=ax3 + bx - 24 chia hết cho (x+1) và (x+3)
\(ax^3+bx-24=\left(x+1\right)Q\left(x\right)\)(1)
\(ax^3+bx-24=\left(x+3\right)P\left(x\right)\) (2) (P(x),Q(x) là các thương)
Thay x = -1 vào (1) và x = -3 vào (2), ta có:
\(\hept{\begin{cases}a.\left(-1\right)^3+b.\left(-1\right)-24=0\\a.\left(-3\right)^3+b.\left(-3\right)-24=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}-a-b=24\\-27a-3b=24\end{cases}}\Rightarrow\hept{\begin{cases}-3a-3b=72\\-27a-3b=24\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}-3a-3b-\left(-27a-3b\right)=72-24\\-a-b=24\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}24a=48\\a+b=-24\end{cases}\Rightarrow}\hept{\begin{cases}a=2\\b=-26\end{cases}}\)
Đúng 0
Bình luận (0)
1. xác định hệ số a,b để:
Đa thức 4x3+ax2+bx+5 chia hết cho đa thức x2-x+1
Xác định các số a và b để đa thức ax^3+bx^2-11x+10 chia hết cho đa thức x^2+x-2
Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$
$x^2+x-2=(x-1)(x+2)$
Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$
$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức)
$\Leftrightarrow a+b-1=-8a+4b+32=0$
$\Leftrightarrow a=3; b=-2$
Đúng 1
Bình luận (0)