Cho nửa đường tròn (O), đường kính BC. Gọi D là điểm cố định thuộc đoạn thẳng OC (D khác O và C). Dựng đường thẳng d vuông góc với BC tại điểm D, cắt nửa đường tròn (O) tại điểm A. Trên cung AC lấy điểm M bất kỳ (M khác A và C), tia BM cắt đường thẳng d tại điểm K, tia CM cắt đường thẳng d tại điểm E. Đường thẳng BE cắt nửa đường tròn (O) tại điểm N (N khác B).1. CM: Tứ giác CDNE nội tiếp một đường tròn2. CM: KE.KDKM.KB và 3 điểm C, K, N thẳng hàng3.Tiếp tuyến tại N của đường tròn(O) cắt đường t...
Đọc tiếp
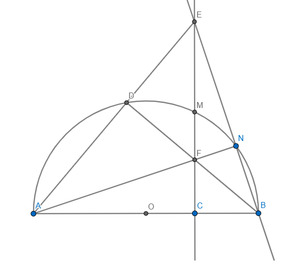
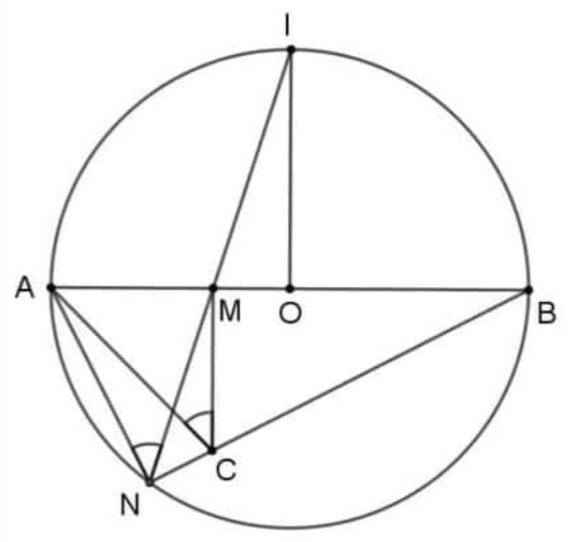
Cho nửa đường tròn (O), đường kính BC. Gọi D là điểm cố định thuộc đoạn thẳng OC (D khác O và C). Dựng đường thẳng d vuông góc với BC tại điểm D, cắt nửa đường tròn (O) tại điểm A. Trên cung AC lấy điểm M bất kỳ (M khác A và C), tia BM cắt đường thẳng d tại điểm K, tia CM cắt đường thẳng d tại điểm E. Đường thẳng BE cắt nửa đường tròn (O) tại điểm N (N khác B).
1. CM: Tứ giác CDNE nội tiếp một đường tròn
2. CM: KE.KD=KM.KB và 3 điểm C, K, N thẳng hàng
3.Tiếp tuyến tại N của đường tròn(O) cắt đường thẳng d tại F. CM: F là trung điểm của CE và EF vuông góc với MN