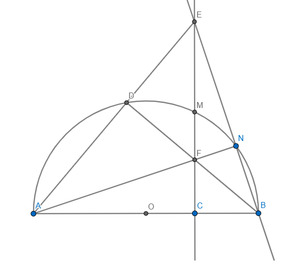
Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A).
a) Chứng minh tứ giác BCFN nội tiếp được một đường tròn.
b) Chứng minh: AD.AE = AC.AB.
a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)