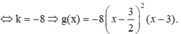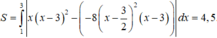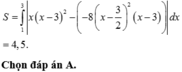Tính x,y ở hình dưới đây biết EF // DG // BC
VV
Những câu hỏi liên quan
Cho
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
và
g
(
x
)
f
(
d
x
+
e
)
với
a
,
b
,
c
,
d
,
e
∈
ℝ
có đồ thị như hình v...
Đọc tiếp
Cho f ( x ) = x 3 + a x 2 + b x + c và g ( x ) = f ( d x + e ) với a , b , c , d , e ∈ ℝ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Diện tích hình phẳng giới hạn bởi hai đường congy=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?
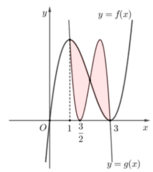
A. 4,5
B. 4,25
C. 3,63
D. 3,67
A B C D E F G H 12 cm y 16 cm Hình vẽ bên, cho biết: AB // CD // EF // GH; AC CE EG;BD DF FH; AB x(cm); CD 12cm; EF y(cm); GH 16cm.Thế thì giá trị của x và y là:
Đọc tiếp
Hình vẽ bên, cho biết: AB // CD // EF // GH; AC = CE = EG;
BD = DF = FH; AB = x(cm); CD = 12cm; EF = y(cm); GH = 16cm.
Thế thì giá trị của x và y là:
Giải:
Hình thang CDHG có: CE = GE , DF = HF ( gt )
=> EF là đường TB của hình thang.
=> EF = \(\dfrac{CD+GH}{2}\) = \(\dfrac{12+16}{2}\) = 14 cm ( hay y = 14 cm )
Hình thang ABFE có: AC = CE, BD = DF ( gt )
=> CD là đường TB của hình thang trên.
=> CD = \(\dfrac{AB+EF}{2}\)
mà CD = 12 cm, EF = 14 cm ( cmt )
=> AB = 12.2 - 14 = 10 cm ( hay x = 10 cm )
Vậy x = 10 cm, y = 14 cm
Đúng 0
Bình luận (0)
Cho ∆ABC có EF // BC (E thuộc AB, F thuộc AC), đường phân giác AD cắt BC tại D, biết AE = 6cm, EB = 3cm, FC = 4cm, DC = 6cm. AF = x, BD = y, EF = z a) Tính x, y b) Tính z
a) Áp dụng định lý Ta-let vào \(\Delta\)ABC, ta có:
\(\frac{AE}{BE}=\frac{AF}{FC}\)
\(\rightarrow\frac{6}{3}=\frac{x}{4}\)
\(\rightarrow x=8\)
Gọi AD là a, ta có:
\(\frac{AF}{FC}=\frac{AD}{DC}\)
\(\rightarrow\frac{6}{3}=\frac{a}{6}\)
\(\rightarrow a=12\)
Vậy:
\(\frac{AE}{BE}=\frac{AD}{BD}\)
\(\rightarrow\frac{6}{3}=\frac{12}{y}\)
\(\rightarrow y=6\)
Áp dụng hệ quả TaLet vào \(\Delta\)ABC, ta có:
\(\frac{EF}{BC}=\frac{AE}{BE}\)
\(\rightarrow\frac{z}{12}=\frac{6}{3}\)
\(\rightarrow z=24\)
Cho
f
x
x
3
+
a
x
2
+
b
x
+
c
và
g
x
f
d
x
+
e
với
a
,
b
,
c
,
d
,
e
∈
R
có đồ thị như hì...
Đọc tiếp
Cho f x = x 3 + a x 2 + b x + c và g x = f d x + e với a , b , c , d , e ∈ R có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x). Diện tích hình phẳng giới hạn bởi hai đường cong y=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?
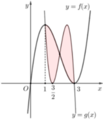
A. 4,5.
B. 4,25.
C. 3,63.
D. 3,67.
Cho tam giác ABC. Trên cạnh AB lấy 2 điểm D và E sao cho AD = DE = EB. Vẽ DG và EF song với BC (G, F thuộc AC) a) Chứng minh AG = GF = FC b) Giả sử DG = 3cm, tính BC
a: Xét ΔAEF có
D là trung điểm của AE
DG//EF
Do đó: G là trung điểm của AF
Suy ra: AG=GF(1)
Xét hìn thang BDGC có
E là trung điểm của BD
EF//GD//BC
Do đó: F là trung điểm của GC
Suy ra: GF=FC(2)
Từ (1) và (2) suy AG=GF=FC
Đúng 1
Bình luận (0)
Bài toán 75
Cho hình vuông ABCD có cạnh 8cm và hình vuông DEFG có cạnh 4cm xếp cạnh nhau như hình vẽ dưới đây. Hãy tính diện tích tam giác ACF?
A B C D E F G 8cm 4cm
S(ACF) = S(ACFG) -S(AFG)
S(ACFG) = S(ACD) + S(CDGF) = \(\frac{8.8}{2}\)+ \(\frac{\left(8+4\right).4}{2}\)= 32 + 24 = 56 (cm2) (1)
S(AFG) = \(\frac{\left(AD+DG\right).GF}{2}\)= \(\frac{\left(8+4\right).4}{2}\)= 24 cm2 (2)
vậy từ (1) và (2) --> S(ACF) = 56 - 24 = 32 cm2
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD). Gọi E;F lần lượt là trung điểm của AD và BC. gọi G là giao điểm của EF và AC. Biết rằng AB = 6cm; CD=8cm.
a) tính EF
b) chứng minh G là trung điểm của AC, tính EG
a, cho hình thanh ABCD(AB//CD). Gọi E,F lần lượt là trung điểm AD Và BC.
Biết AB=8cm: CD=12cm. Tính độ dài EF.
b, Cho hình thang ABCD(AB//CD). Gọi E,F lần lượt là trung điểm AD và BC.
Biết AB=10cm: EF=16cm. Tính độ dài CD.
Cho tam giác ABC. Trên cạnh AB lấy 2 điểm D và E sao cho AD=DE=EB. Vẽ DG và EF song song với BC (G, F thuộc AC)\
a, CM AG=GF=FC
b, giả sử DG=3cm tính bc
Bài 1: Thực hiện phép tính (Tính hợp lý nếu có thể):
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
¬
Bài 2: Tìm x biết:
a)
b)
c)
d)
e)
f)
g) ¬¬
h)
i)
j)
k)
l)
Bài 3: Tìm x, y, z biết:
a) và
b) và
c) và
d) và
e) và
f) và
g) và
h) và
Cứu !!!
Xem chi tiết


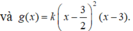 .
.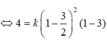 .
.