1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
NQ
Những câu hỏi liên quan
Cho
log
3
2
a
;
log
3
5
b
Giá trị của biểu thức
P
log
3
60
tính theo a và b là A. Pa+b-1 B. Pa-b-1 C. P2a+b+1 D. Pa+2b+1
Đọc tiếp
Cho log 3 2 = a ; log 3 5 = b Giá trị của biểu thức P = log 3 60 tính theo a và b là
A. P=a+b-1
B. P=a-b-1
C. P=2a+b+1
D. P=a+2b+1
Cho log3 5 a, log3 6 b, log3 22 c. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho log3 5 = a, log3 6 = b, log3 22 = c. Mệnh đề nào dưới đây đúng?
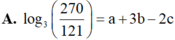
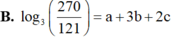
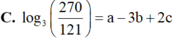
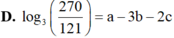
Cho log3=a, log5=b. Tính \(\log_{15}\)30 theo a và b
Bạn nào muốn luyện thêm Logarit thì có thể vào website http://tailieutracnghiem.net ấy
Đúng 0
Bình luận (0)
Log cơ số 15 của 30 = log cơ số 10 của 30 chia log cơ số 10 của 15 . sau đó bạn phân tích log cơ số 10 ( 3.5) chia cho log cơ số 10 của (3.10) . tiếp đó bạn áp dụng công thức log cơ số a của b1. b2= log cơ số a của b1+ log cơ số a của b2. Bạn làm như thế rồi diệt trừ hết sau đó thay vào là được . Đáp án là a+b chia a+1
Đúng 0
Bình luận (3)
Đặt a log3 5, b log4 5. Hãy biểu diễn log15 10 theo a và b.
Đọc tiếp
Đặt a = log3 5, b = log4 5. Hãy biểu diễn log15 10 theo a và b.
Cho
log
2
a
,
log
3
b
. Biểu diễn
log
625
270
theo a và b là A.
a
+
b
2
2
a
1
−
b...
Đọc tiếp
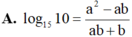
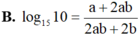
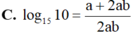
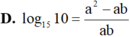
Cho log 2 = a , log 3 = b . Biểu diễn log 625 270 theo a và b là
A. a + b 2 2 a 1 − b x
B. a + b 2 3 a 1 − b
C. a + b 2 4 a 1 − b
D. 1 4 3 b + 1 1 − a
Biết phương trình
log
3
3
x
-
1
1
+
log
3
3
x
-
1...
Đọc tiếp
Biết phương trình log 3 3 x - 1 1 + log 3 3 x - 1 = 6 có hai nghiệm là x 1 < x 2 và tỉ số x 1 x 2 = log a b trong đó a , b ∈ ℕ và a,b có ước chung lớn nhất bằng 1. Tính a + b
A. a + b = 38
B. a + b = 37
C. a + b = 56
D. a + b = 55
Với hai số thực dương a, b tùy ý và
log
3
5
.
log
5
a
1
+
log
3
2
-
log
6
b...
Đọc tiếp
Với hai số thực dương a, b tùy ý và log 3 5 . log 5 a 1 + log 3 2 - log 6 b = 2 . Khẳng định nào dưới đây là khẳng định đúng?
A. a = blog6 2
B. a = 36b
C. 2a + 3b = 0
D. a = blog6 3
Cho
P
l
o
g
3
(
a
2
b
3
)
(a,b là các số dương). Khẳng định nào sau đây là đúng ? A.
P
6
l
o
g
3
a
.
log
3
b
B.
P
2
log
3...
Đọc tiếp
Cho P = l o g 3 ( a 2 b 3 ) (a,b là các số dương). Khẳng định nào sau đây là đúng ?
A. P = 6 l o g 3 a . log 3 b
B. P = 2 log 3 a + 3 log 3 b
C. P = ( 1 / 2 ) log 3 a + ( 1 / 3 ) log 3 b
D. P = ( log 3 a ) 2 . ( log 3 b ) 3
Cho log5a5 và log3 b 2/3. Tính giá trị biểu thức I 2 log6[ log5 (5a)] + log1/9 b3 A. B. C. D.
Đọc tiếp
Cho log5a=5 và log3 b= 2/3. Tính giá trị biểu thức I= 2 log6[ log5 (5a)] + log1/9 b3
A. 
B. 
C. 
D. 
Cho a là số thực a ≠ 1 và log3\(\sqrt[]{}\)a a3 . Mệnh đề nào sau đây đúng?
A. P = 1/3
B. P = 3
C. P = 1
D. P = 9