cho tam giác abc có góc abc 45 độ acb= 30 gọi M là trung điểm của AC . Tính số đo của góc AMB
NK
Những câu hỏi liên quan
1. Cho tam giác ABC có góc B=45 độ, góc C=30 độ , BM là đường trung tuyến của tam giác ABC. Tính số đo góc AMB
2. Cho tam giác ABC có AB=6cm, AC=10cm, độ dài đường trung tuyến AM=4cm. Tính diện tích tam giác ABC
Đề bài: Cho tam giác vuông ABC có góc A 90 độ, BC 2A. Gọi O là trung điểm của BC, dựng AH vuông góc với BC.a. Khi góc ACB 30 độ, tính độ dài các cạnh còn lại của tam giác.b. Khi góc ACB 30 độ, gọi M là trung điểm của AC. Tính độ dài BM.c. Khi góc ACB 30 độ, các đoạn thẳng AO và BM cắt nhau tại điểm G. Tính độ dài GC.Giúp mình với tối nay mình cần rồi, cảm ơn trước ạ.❤
Đọc tiếp
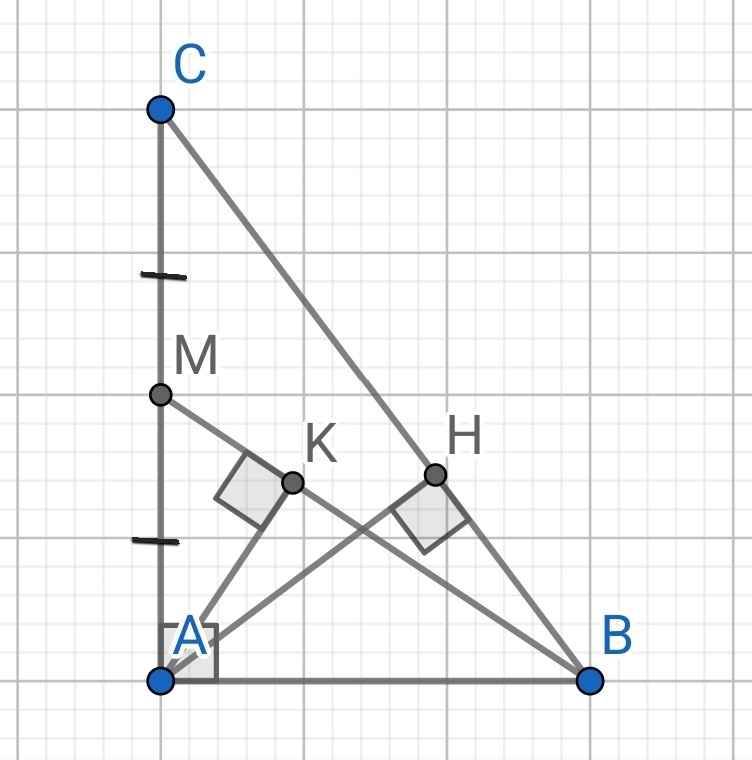
Đề bài: Cho tam giác vuông ABC có góc A = 90 độ, BC = 2A. Gọi O là trung điểm của BC, dựng AH vuông góc với BC.
a. Khi góc ACB = 30 độ, tính độ dài các cạnh còn lại của tam giác.
b. Khi góc ACB = 30 độ, gọi M là trung điểm của AC. Tính độ dài BM.
c. Khi góc ACB = 30 độ, các đoạn thẳng AO và BM cắt nhau tại điểm G. Tính độ dài GC.
Giúp mình với tối nay mình cần rồi, cảm ơn trước ạ.❤
a, Khi ![]() thì tam giác ABC là tam giác nửa đều nên
thì tam giác ABC là tam giác nửa đều nên  ,
,
![]() .
.
b, Theo câu a) ta có: 
 .
.
c. Do G là trọng tâm của tam giác ABC nên  (với N là trung điểm của AB).
(với N là trung điểm của AB).
Áp dụng định lí Pitago ta có:  . Suy ra
. Suy ra  .
.
d. Ta có:  . Diện tích tam giác AHO lớn nhất khi và chỉ khi
. Diện tích tam giác AHO lớn nhất khi và chỉ khi ![]() . Tức là AHO vuông cân tại H. Suy ra
. Tức là AHO vuông cân tại H. Suy ra ![]()
e. Tứ giác AMON là hình chữ nhật nên ![]() . Theo bất đẳng thức Côsi ta có:
. Theo bất đẳng thức Côsi ta có:
![]() . Mà
. Mà ![]() nên
nên  . Vậy
. Vậy  . Dấu bằng xảy ra khi và chỉ khi
. Dấu bằng xảy ra khi và chỉ khi ![]() , hay tam giác ABC vuông cân tại A.
, hay tam giác ABC vuông cân tại A.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn ; BH=4cm và HC=6cm
a) Tính độ dài các đoạn AH,AB,AC
b) Gọi M là trung điểm của AC . Tính số đo góc AMB ( làm tròn đến độ )
c) Kẻ AK vuông góc với BM ( K thuộc BM ) . Chứng minh BK.BM=BH.BC
1) Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn: BH=4cm và HC=6cm
a) Tính độ dài các đoạn AH,AB,AC
b) Gọi M là trung điểm của AC. Tính số đo góc AMB( làm tròn đến độ )
c) Kẻ AK vuông góc với BM (K thuộc BM) . Chứng minh : BK.BM=BH.BC
Vẽ hình luôn ah
a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)
Đúng 2
Bình luận (4)
Cho tam giác ABC vuông tại A có góc ABC=60độ.
a)Tính số đo góc ACB và so sánh độ dài hai cạnh AB, AC
b) Gọi M là trung điểm AC. Kẻ đường thẳng vuông góc với AC tại M, đường thẳng này cắt BC tại N, Chứng minh tam giác AMN= tam giác CMN
c)Chứng minh tam giác ABN là tam giác đều
d)Gọi G là giao điểm của AN và BM, Chứng minh BC=6.GN
Giải hộ mình câu cuối phần d nha, 😊
Đúng 0
Bình luận (1)
cho tam giác abc vuông cân tại a m là trung điểm của bc . Gọi M là trung điểm của BC . Trên tia đới của tia MA lấy điểm E sao cho ME= MA
a,tính số đo của góc ABC khi góc ACB=40 độ.
b,chứng minh tam giác AMB = EMC và AB//EC
c,từ C kẻ đường thẳng song song với AE. Kẻ EK vuông góc đường thẳng tại K.Chứng minh: góc KEC =BCA
Bạn gõ thừa chữ "cân"
a/ Xét t/g ABC vuông tại A có
\(\widehat{ABC}+\widehat{ACB}=90^o\) (t/c)
\(\Rightarrow\widehat{ABC}=90^o-40^o=50^o\)
b/ Xét t/g AMB và t/g EMC có
AM = EM
\(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)MB = MC
=> t/g AMB = t/g EMC (c.g.c)c/ Có
AE // CK
=> \(\widehat{AEK}+\widehat{EKC}=180^o\) (tcp)
=> \(\widehat{AEK}=\widehat{AEC}+\widehat{CEK}=90^o\)
Xét t/g ABC vuông tại A có AM là đường trung tuyến
=> AM = 1/2 BC = BM
=> t/g AMB cân tại A
=> \(\widehat{ABC}=\widehat{BAM}\)
Mà \(\widehat{BAM}=\widehat{CEA}\)
=> \(\widehat{CBA}+\widehat{CEK}=90^o\)
=> \(\widehat{CEK}=\widehat{ACB}\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a) Tính số đo của góc ABC khi góc ACB=40 độ
b) Chứng minh: tam giác AMB = tam giác EMC và AB // EC.
c) Từ C kẻ đường thẳng (d) song song với AE. Kẻ EK vuông góc đường thẳng (d) tại K. Chứng minh: góc KEC= góc BCA .
cho tam giác ABC có góc BAC 50 độ, góc ACB 70 độ. lấy điểm I nằm trong tam giác ABC sao cho góc IBC 30 độ, góc ICB 35 độ.a) tính số đo góc ABC; b) chứng minh rằng các tia BI, CI lần lượt là tia phân giác của góc ABC, ACB; c) gọi D, E, F lần lượt là hình chiếu vuông góc của điểm I trên các đường thẳng BC, CA, AB. Chứng minh rằng I là giao điểm của 3 đường trung trực của tam giác DEF
Đọc tiếp
cho tam giác ABC có góc BAC =50 độ, góc ACB =70 độ. lấy điểm I nằm trong tam giác ABC sao cho góc IBC =30 độ, góc ICB =35 độ.
a) tính số đo góc ABC; b) chứng minh rằng các tia BI, CI lần lượt là tia phân giác của góc ABC, ACB; c) gọi D, E, F lần lượt là hình chiếu vuông góc của điểm I trên các đường thẳng BC, CA, AB. Chứng minh rằng I là giao điểm của 3 đường trung trực của tam giác DEF
a: góc ABC=180-50-70=60 độ
b: Vì góc IBC=1/2*góc ABC
nên BI là phân giác của góc ABC
Vì góc ICB=1/2*góc ACB
nên CI là phân giác của góc ACB
c: Xét ΔBFI vuông tại F và ΔBDI vuông tại D có
BI chung
góc FBI=góc DBI
=>ΔBFI=ΔBDI
=>ID=IF
Xét ΔCDI vuông tại D và ΔCEI vuông tại E co
CI chung
góc DCI=góc ECI
=>ΔCDI=ΔCEI
=>ID=IE=IF
=>I là giao của 3 đường trung trực ΔDEF
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A=90 độ, góc B =30 độ. Gọi M là trung điểm của BC. Tính số đo góc BAM

Do M là trung điểm của BC và \(\Delta ABC\) vuông tại A
\(\Rightarrow AM\) là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow AM=BM=CM=\dfrac{BC}{2}\)
\(\Rightarrow\Delta MAB\) cân tại M
\(\Rightarrow\widehat{BAM}=\widehat{ABM}=30^0\)
Đúng 1
Bình luận (0)