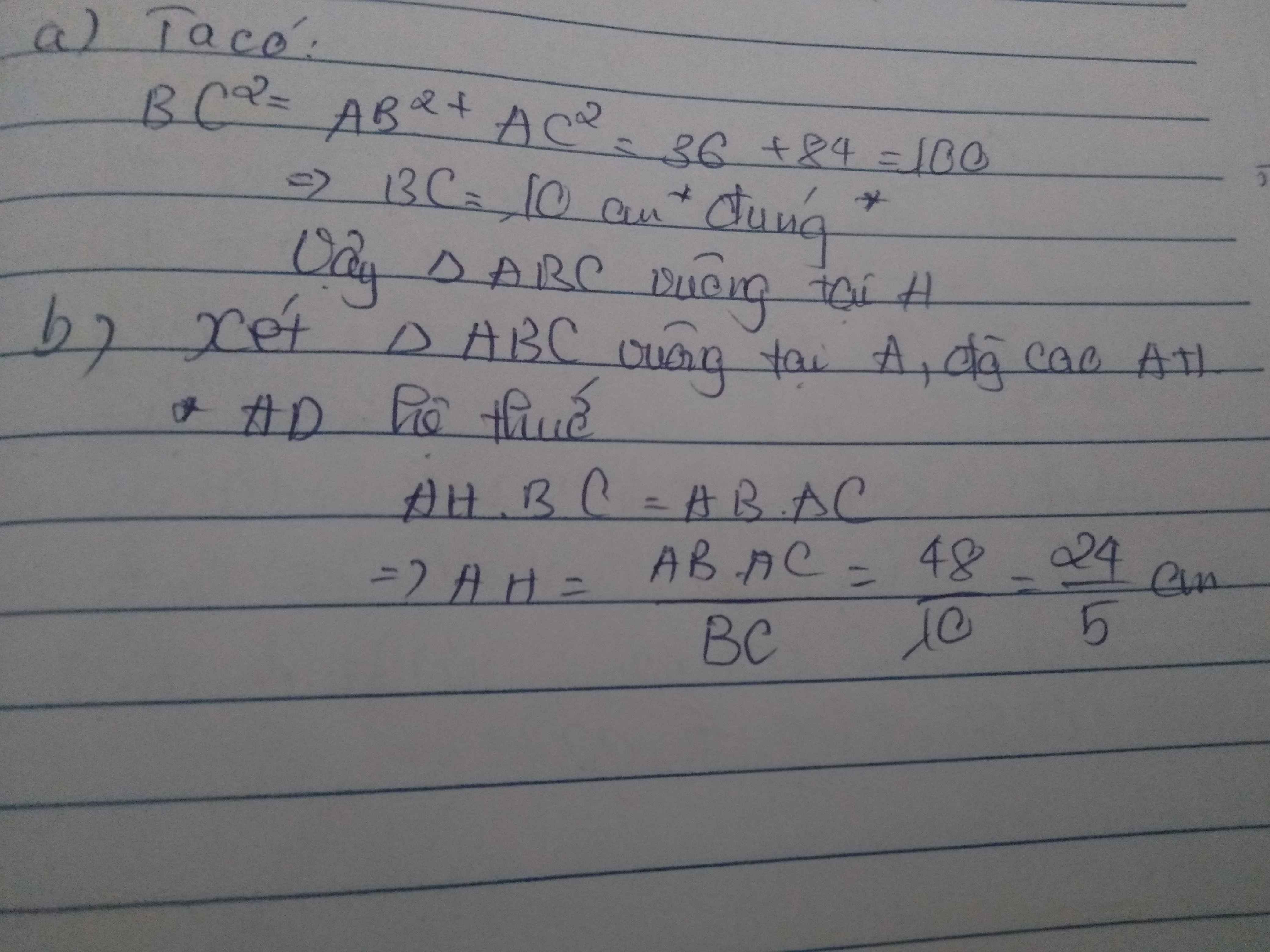ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)-bài 1: cho tam giác ABC có AB6cm; AC8cm; BC10cm.a, chứng minh tam giác ABC vuôngb, tính độ cao AH-bài 2: cho tam giác ABC có, AB12cm; AC16cm; BC20cma, chứng minh tam giác ABC vuôngb tính độ cao AHc, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC3:5 và AB15cma, tính HB và HC b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.ACEF.BC-bài 4:...
Đọc tiếp
ai giúp mình giải bài toán này với được k ạ ( chi tiết hộ mình nhé)
-bài 1: cho tam giác ABC có AB=6cm; AC=8cm; BC=10cm.
a, chứng minh tam giác ABC vuông
b, tính độ cao AH
-bài 2: cho tam giác ABC có, AB=12cm; AC=16cm; BC=20cm
a, chứng minh tam giác ABC vuông
b tính độ cao AH
c, kẻ HD và HE lần lượt vuông góc AB , AC. Tính HD và HE.
-Bài 3: cho tam giác ABC vuông tại A , đường cao AH, biết AH:AC=3:5 và AB=15cm
a, tính HB và HC
b, gọi E, F lần lượt là hình chiếu của H trên AB và AC ; chứng minh AB.AC=EF.BC
-bài 4: cho tam giác ABC vuông tại A đường phân giác trong BD( DϵAC) cho AB=3cm; BC=5cm.
a, tính AC, AD,CD
b, tính BD