Chứng minh rằng: a2 + b2 -2ab +1 > 0 với mọi số a,b
Cảm ơn trước ạ!
Chứng minh rằng nếu: a/b = b/c thì a2 + b2/b2 + c2 = a/b( Với b,c # 0).
Giúp mk với ạ! Mk cảm ơn
Chứng minh rằng:
52005 + 52003 chia hêt cho 13
b) a2 + b2 + 1 ≥ ab + a + b
Cho a + b + c = 0. chứng minh:
a3 + b3 + c3 = 3abc
![]() Các cao nhân giúp em ạ
Các cao nhân giúp em ạ![]()
em cảm ơn trước![]()
1) 52005 +52003 = 52003(52+1)=52003(25+1) = 52003.26
Mà 26 chia hết cho 13 => ...
2)a2 + b2 + 1 ≥ ab + a + b <=> 2a2+2b2+2 ≥ 2ab + 2a +2b (*nhân cả hai vế với 2*)
<=> 2a2-2ab+2b2 +2 -2a -2b ≥0 (*chuyển vế phải sang vế trái và đổi dấu*)
<=> (a2-2ab+b2)+(a2-2a+1)+(b2-2b+1)≥0
<=> (a-b)2+(a-1)2+(b-1)2≥0
=> Bất đẳng thức đúng
=> đpcm
3) Ta có a+b+c=0
<=> a+b = -c
<=> (a+b)3=(-c)3
<=> a3+3a2b+3ab2+b3= -c3
<=> a3+b3+c3= -3a2b -3ab2 (*chuyển vế*)
<=> a3+b3+c3= -3ab(a+b) = -3ab(-c)=3abc (*do a+b = -c*)
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 - 2 a b ≥ 0
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
cho a, b, c là các số thực. Chứng minh rằng: a2 + b2 + c2 ≥ 2ab - 2bc +2ca
BĐT cần chứng minh tương đương:
\(a^2+b^2+c^2\ge2ab-2bc+2ca\)
\(\Leftrightarrow a^2+b^2+c^2+2bc-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow a^2+\left(b+c\right)^2-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow\left(a-b-c\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
Chứng minh các đẳng thức sau:
a ) 1 − a a 1 − a + a 1 − a 1 − a 2 = 1 v ớ i a ≥ 0 v à a ≠ 1 b ) a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = | a | v ó i a + b > 0 v à b ≠ 0
a) Biến đổi vế trái:
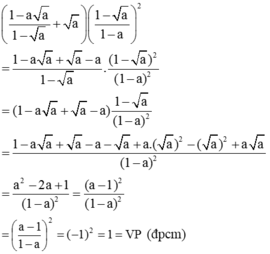
b) Biến đổi vế trái:
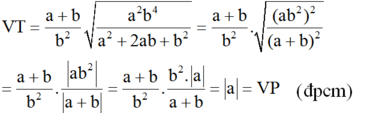
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )
Câu 6: ( 0,5 điểm)
Chứng minh rằng nếu a, b, c là ba cạnh của một tam giác thì:
a2+ b2+ c2 - 2ab -2bc- 2ac < 0
Vì a,b,c là 3 cạnh tam giác nên \(a+b>c\Leftrightarrow ac+bc>c^2\)
CMTT: \(ab+bc>b^2;ab+ac>a^2\)
Cộng vế theo vế \(\Leftrightarrow a^2+b^2+c^2< ab+bc+ca+ab+bc+ca\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\\ \Leftrightarrow a^2+b^2+c^2-2ab-2bc-2ca< 0\)
Cho a + b + c = a2 + b2 + c2 = 1 và\(\dfrac{x}{a}\)=\(\dfrac{y}{b}\)=\(\dfrac{z}{c}\)( a≠0,b≠0,c≠0 )
Chứng minh rằng (x+y+z)2=x2+y2+z2
Giúp mình với ạ, mai mình thi rồi !!!!![]()
6. Chứng minh rằng:
a. x2 + xy + y2 + 1 > 0 với mọi x, y
b. x2 + 4y2 + z2 - 2x - 6z + 8y + 15 > 0 Với mọi x, y, z
(ai lm giúp với ạ iem cảm ơn nhìu
a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)
b.
$x^2+4y^2+z^2-2x-6z+8y+15=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1$
$=(x-1)^2+(2y+2)^2+(z-3)^2+1\geq 0+0+0+1>0$ với mọi $x,y,z$
Ta có đpcm.