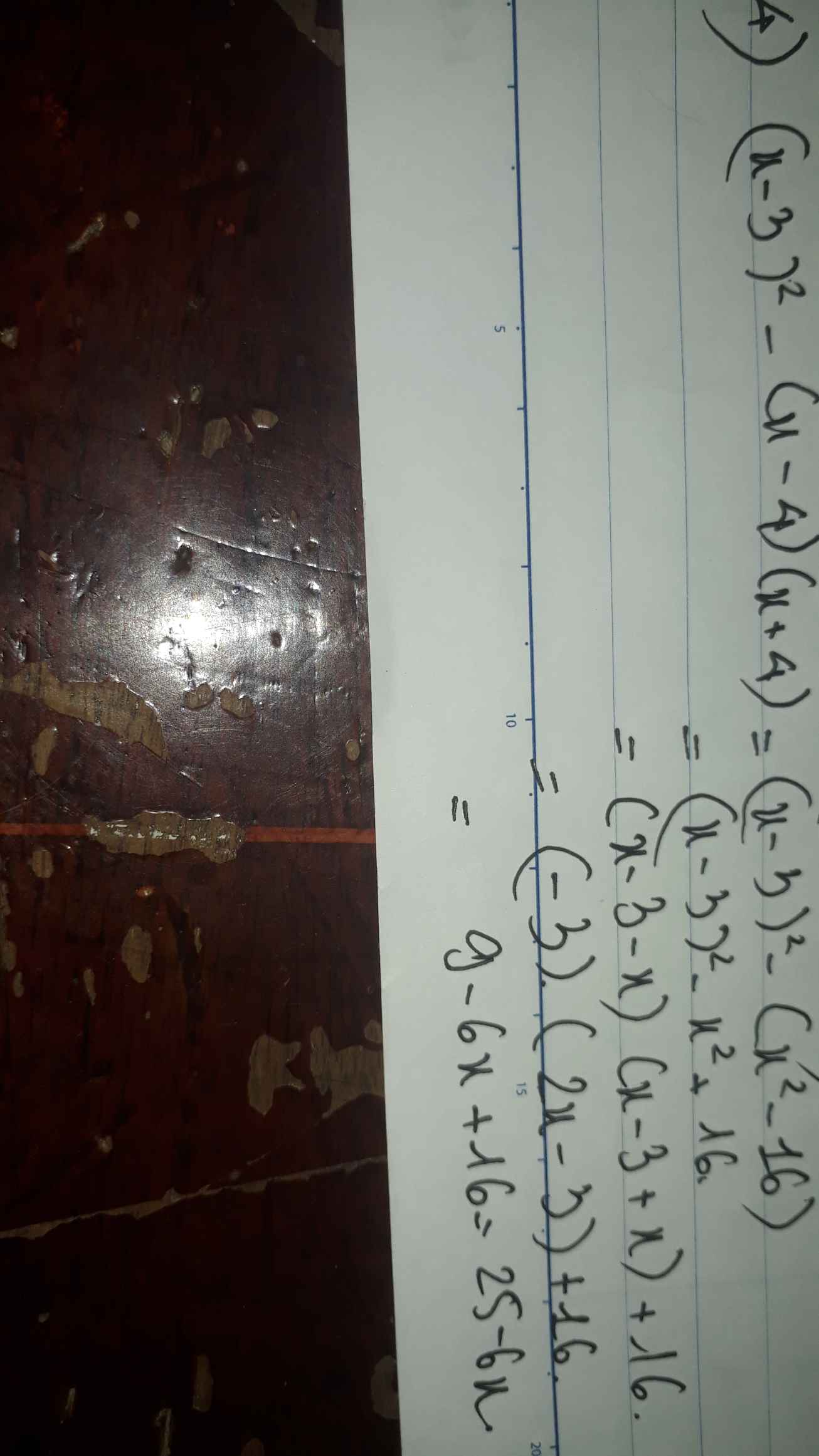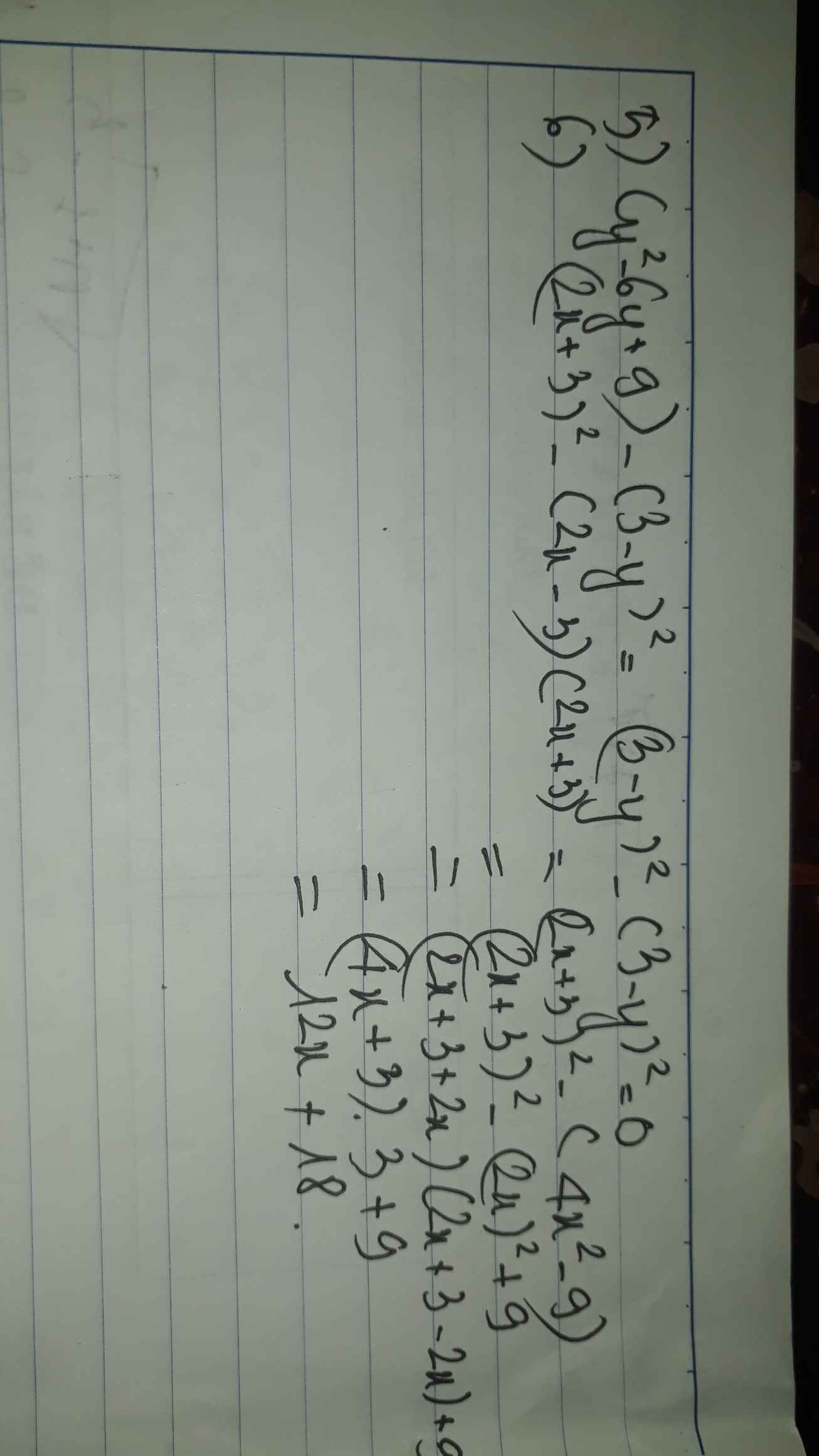(2x+1) (y-5)=19
TH
Những câu hỏi liên quan
Giải hệ \(\left\{{}\begin{matrix}3x+2y=19\\\sqrt{\dfrac{2x-3}{y+5}}+\sqrt{\dfrac{y+5}{2x-3}}=-1\end{matrix}\right.\)
Lời giải:
Đặt $\sqrt{\frac{2x-3}{y+5}}=t$ thì pt số 2 trở thành:
$t+\frac{1}{t}=-1$
$\Leftrightarrow t^2+t+1=0$
$\Leftrightarrow (t+0,5)^2=-0,75<0$ (vô lý)
Do đó pt vô nghiệm.
Đúng 2
Bình luận (2)
Nếu đề đổi như bên dưới thì:
\(t+\frac{1}{t}=2\Rightarrow t^2-2t+1=0\)
$\Leftrightarrow (t-1)^2=0\Leftrightarrow t=1$
$\Rightarrow 2x-3=y+5$
$\Leftrightarrow 2x-y=8$
Kết hợp với $3x+2y=19$ thì đây là bài toán giải hệ 2 ẩn thông thường thôi
$x=5; y=2$ (tm)
Đúng 2
Bình luận (0)
Bài 19 Rút gọn
1) (x+2)^2+(3-x)^2
2) (4-x)^2 -(x-3)^2
3) (x-5)(x+5)-(x+5)^2
4) (x-3)^2-(x-4)(x+4)
5) (y^2 -6y+9)-(3-y)^2
6. (2x+3)² –(2x–3).(2x+3)
1) Ta có: \(\left(x+2\right)^2+\left(x-3\right)^2\)
\(=x^2+4x+4+x^2-6x+9\)
\(=2x^2-2x+13\)
2) Ta có: \(\left(4-x\right)^2-\left(x-3\right)^2\)
\(=\left(4-x-x+3\right)\left(4-x+x-3\right)\)
\(=-2x+7\)
3) Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)^2\)
\(=x^2-25-x^2-10x-25\)
=-10x-50
Đúng 3
Bình luận (0)
4) Ta có: \(\left(x-3\right)^2-\left(x-4\right)\left(x+4\right)\)
\(=x^2-6x+9-x^2+16\)
=-6x+25
5) Ta có: \(\left(y^2-6y+9\right)-\left(y-3\right)^2\)
\(=y^2-6y+9-y^2+6y-9\)
=0
6) Ta có: \(\left(2x+3\right)^2-\left(2x-3\right)\left(2x+3\right)\)
\(=4x^2+12x+9-4x^2+9\)
=12x+18
Đúng 2
Bình luận (0)
Bài 19 rút gọn
1) (x+2)^2+(3-x)^2
2) (4-x)^2-(x-3)^2
3) (x-5)(x+5)-(x+5)^2
4)(x-3)^2-(x-4)(x+4)
5) (y^2-6y+9)-(3-y)^2
6) (2x+3)^2-(2x-3)(2x+3)
1) Ta có: \(\left(x+2\right)^2+\left(x-3\right)^2\)
\(=x^2+4x+4+x^2-6x+9\)
\(=2x^2-2x+13\)
2) Ta có: \(\left(4-x\right)^2-\left(x-3\right)^2\)
\(=\left(4-x-x+3\right)\left(4-x+x-3\right)\)
\(=\left(-2x+7\right)\cdot1\)
\(=-2x+7\)
3) Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)^2\)
\(=x^2-25-x^2-10x-25\)
\(=-10x-50\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
A= ( 4x - 5)(2x+3) - 4(x+2)(2x - 1)+(10x+7)
B=(7x - 6y)(4x+3y) - 2(14x+y)(x - 9y) - 19(13xy - 1)
Tìm x,y,z : 2x=3y ; 5y=7z và 3x+5z-7y=30 x^2/5=y^2/4 và x^2-y^2=1 x/19=y/21 và 2x-y=34 Giúp mình với😭😭😭
câu 1:
2x=3y =>\(\dfrac{x}{3}=\dfrac{y}{2}\) (1)
5y=7z =>\(\dfrac{y}{7}=\dfrac{z}{5}\) (2)
Từ (1) và (2) suy ra
\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)=\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Dựa vào tính chất dãy tỉ số bằng nhau
Suy ra \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)=\(\dfrac{3x+5z-7y}{63+50-98}=\dfrac{30}{15}=2\)
\(\dfrac{x}{21}=2\) =>x=2.21=42
\(\dfrac{y}{14}=2\) =>y=2.14=28
\(\dfrac{z}{10}=2\) =>z=2.10=20
Vậy x=42;y=28 và z=20
Đúng 0
Bình luận (0)
Câu 2:
\(\dfrac{x^2}{5}=\dfrac{y^2}{4}\)
Dựa vào tính chất dãy tỉ số bằng nhau
Suy ra \(\dfrac{x^2-y^2}{5-4}\) =\(\dfrac{1}{1}=1\)
\(\dfrac{x^2}{5}=1\) =>x2=1.5=5 =>x=\(\sqrt{5}\) hay -\(\sqrt{5}\)
\(\dfrac{y^2}{4}=1\) => y2=1 => y=1 hay -1
Đúng 0
Bình luận (0)
2x/3=3y/5.Tính 19+x/x+y=?
tìm x ; y
biết x+y=5
2x+5y=19
x+y=5
<=>2(x+y)=2*5
<=>2x+2y=10
Mà 2x+5y=19
=>2x+5y-2x-2y=19-10
<=>3y=9
<=>y=3
Thay vào x+y=5
=>x=2
Vậy:...
Đúng 0
Bình luận (0)
câu 3: giải hệ phương trìnha) left{{}begin{matrix}5a+b5b-10a-19end{matrix}right.b) left{{}begin{matrix}dfrac{5x}{6}-ydfrac{-5}{6}dfrac{2x}{2x+y}+3ydfrac{-2}{3}end{matrix}right.c)left{{}begin{matrix}xsqrt{3}+3y12x-ysqrt{3}sqrt{3}end{matrix}right.d) left{{}begin{matrix}dfrac{1}{x}-dfrac{6}{y}dfrac{5}{x}+dfrac{6}{y}13end{matrix}right.17giúp mk vs ạ mk cần gấp
Đọc tiếp
câu 3: giải hệ phương trình
a) \(\left\{{}\begin{matrix}5a+b=5\\b-10a=-19\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\dfrac{5x}{6}-y=\dfrac{-5}{6}\\\dfrac{2x}{2x+y}+3y=\dfrac{-2}{3}\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}x\sqrt{3}+3y=1\\2x-y\sqrt{3}=\sqrt{3}\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{6}{y}\\\dfrac{5}{x}+\dfrac{6}{y}=13\end{matrix}\right.=17\)
giúp mk vs ạ mk cần gấp
a) \(\left\{{}\begin{matrix}5a+b=5\\b-10a=-19\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5a+b=5\\15a=24\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{8}{5}\\b=-3\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{6}{y}=17\\\dfrac{5}{x}+\dfrac{6}{y}=13\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{6}{y}=17\\\dfrac{6}{x}=30\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1. Rút gọn: M = [(x^5)-(2x^4)+(2x^3)-(4x^2)+3x+6]/[(x^2)+2x-8]
2. Cho a, b, c thỏa mãn: (1/a)+(1/b)+(1/c)=1/(a+b+c)
Chứng minh rằng: M = [(a^19)+(b^19)].[(b^5)+(c^5)].[(c^2001)+(a^2001)]=0
3. Cho a, b, c, x, y, z thỏa mãn: a+b+c=1; (a^2)+(b^2)+(c^2)=1 và 1/a=1/b=1/c
Chứng minh rằng: xy+yz+xz=0