áp dụng định lí pytago cho tam giác abc vuông tại a

\(BC^2=\sqrt{AB^2+AC^2}=3\sqrt{34}\)

do AD là tia phân giác góc A nên

\(\dfrac{CD}{BD}=\dfrac{AC}{AB}=\dfrac{5}{3}\)

suy ra CD=\(\dfrac{15.\sqrt{34}}{8}\)

kẻ đường cao AH

suy ra \(AD^2=HD^2+AH^2\)

ta có AH.BC=AB.AC suy ra \(AH=\dfrac{45}{\sqrt{34}}\)

\(CH.BC=CA^2=225\) suy ra \(CH=\dfrac{75}{\sqrt{34}}\) 

suy ra \(HD=CH-CD=...\)

thay vào tính được \(AD^2\) rồi tính dc AD

 

xét ΔABC và ΔDBN ta có

\(\widehat{B}\)  chung

\(\widehat{BAC}=\widehat{BDN}=90^o\)

=>ΔABC∼ΔDBN(g.g)

=>\(\dfrac{BA}{BD}=\dfrac{BC}{BN}\)

=>\(BA.BN=BD.BC\)

 

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có

BD chung

góc ABD=góc HBD

=>ΔBAD=ΔBHD

b: ΔBAD=ΔBHD

=>DA=DH

mà DH<DC

nên DA<DC

c: Xét ΔDAK vuông tại A và ΔDHC vuông tại H có

DA=DH

AK=HC

=>ΔDAK=ΔDHC

=>góc ADK=góc HDC

=>góc HDC+góc KDC=180 độ

=>K,D,H thẳng hàng

bạn nào có lời giải bài này thì cho mk xin vs ạ :<

a: Đề sai rồi bạn

b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

\(\widehat{ABE}=\widehat{HBE}\)

Do đó: ΔBAE=ΔBHE

Suy ra: BA=BH

c: Ta có: \(\widehat{CAH}+\widehat{BAH}=90^0\)

\(\widehat{MAH}+\widehat{BHA}=90^0\)

mà \(\widehat{BAH}=\widehat{BHA}\)

nên \(\widehat{CAH}=\widehat{MAH}\)

hay AH là tia phân giác của góc MAC

Xin lỗi mình không thể chụp ảnh.

Phần 5 thì chỉ có AE song song với CF thôi nhé. Còn BD vuông góc với CF.

1. Xét tam giác ABD và tam giác EBD có:

BAD=BED=90^o (gt)

ABD= EBD( BD là tia phân giác)

BD chung ( gt)

=> 2 tam giác = nhau

=> AB=BE ( 2 cạnh tương ứng)

Xét tam giác EBF và tam giác ABC có:

B1=B2(cmt)

A=E  (cmt)

BE=BA( cmt)

=> 2 tam giác = nhau

2. Trong tam giác cân, tia phân giác xuất phát từ đỉnh đồng thời là đường trung trực. => BH vuông góc với AE và H là trung điểm của AE( tính chất đường trung trực) (đpcm)

3.Ta có: AD=ED( tam giác ABD= EBD) (1)

Mặt khác, DC> ED( cạnh huyền lớn hơn cạnh góc vuông) (2)

Từ (1)và (2) => DC>AD ( đcpm)

Ý 2:

Có: BA=BE(cmt)

BF=BC( tam giác BFE= BCA)

và BC= BE+EC ; BF= AB+AF

=> AF= EC

=> Tam giác BFC cân

5. Gọi giao của BH và FC là G.

Có tam giác BFC cân( cmt)

=> BG vuông góc với FC ( trong tam giác cân, tia phân giác đồng thời là đường trung tuyến)

Mặt khác,BH vuông góc với AE

=> AE song song FC ( từ vuông gó đến song song)

Nhớ tim và cảm ơn nhé. cảm ơn bạn. Chúc bạn học tốt.

 

a) Xét tam giác ABD và tam giác ACE có 
góc ADB = góc AEC = 90 độ 
AB=AC 
góc A: chung 
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn) 
=> BD=CE và AD=AE 
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD 
Xét tam giác OEB và tam giác ODC có 
góc OEB = góc ODC = 90 độ 
BE=CD 
góc BOE = góc COD (đối đỉnh) 
=> tam giác OEB = tam giác ODC => OB=OC 
c) Xét tam giác AOB và tam giác AOC có 
AB=AC 
OB=OC 
AO: cạnh chung 
=> tam giác AOB = tam giác AOC (c.c.c) 
=> góc OAB=góc OAC 
=> AO la tia phân giác góc BAC

Bài mk lm như dzị ak

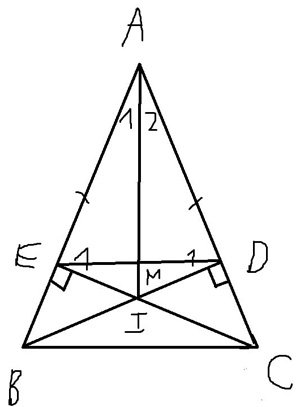a, tg ADB và tg AEC có
^E1 = ^D1 = 90 độ
AB = AC 
^A chung
=> tg ADB = tg AEC
=> AD = AE
=> tg ADE cân
b, tg ABI và tg ACI có
^E1 = ^D1 = 90 độ
AI chung
 AB = AC
=> tg ABI = tg ACI 
=> ^A1 = ^A2 ( góc t/ứ)
=> IB = IC ( cạnh t/ứ)
=> tg IBC cân
c, vì ^A1 = ^A2 ( câu b )
=> AI là tpg của góc EAD