Gọi x; y; z là độ dài ba cạnh tam giác vuông với z là cạnh huyền thì theo đề bài,ta có: 

\(z>y\ge x\ge1\) và

\(\hept{\begin{cases}x^2+y^2=z^2\left(\text{Định lí Pythagoras}\right)\\\frac{xy}{2}=x+y+z\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(x+y\right)^2-2xy=z^2\left(1\right)\\xy=2\left(x+y+z\right)\left(2\right)\end{cases}}\)   

Thay (2) lên (1) suy ra \(z^2=\left(x+y\right)^2-4\left(x+y+z\right)\)

\(\Leftrightarrow z^2+4z=\left(x+y\right)^2-4\left(x+y\right)\)

\(\Leftrightarrow z^2+4z+4=\left(x+y\right)^2-4\left(x+y\right)+4\)

\(\Leftrightarrow\left(z+2\right)^2=\left(x+y-2\right)^2\) (*)

Do \(z>y\ge x\ge1\) nên cả hai vế cùng không âm.

Do đó từ (*) suy ra \(z+2=x+y-2\Leftrightarrow z=x+y-4\)

Thay ngược lên (2) và giải tiếp bằng cách phân tích đa thức thành nhân tử và lập bảng xét ước:P.

Note: Em không chắc đâu ạ!

Tam giác ABO là tam giác đều nên \(\widehat {ABO} = \widehat {AOB} = \widehat {BAO} = 60^\circ \). Vậy \(x = 60^\circ \).

Ba điểm B, O, C thẳng hàng nên \(\widehat {BOC} = 180^\circ \). Mà \(\widehat {AOB} = 60^\circ \)nên \(\widehat {AOC} = 180^\circ  - 60^\circ  = 120^\circ \).

Xét tam giác AOC có OA = OC. Vậy tam giác AOC cân tại O nên \(\widehat{OAC} = \widehat{OCA} =\dfrac{1}{2}. (180^0-\widehat{AOC})= \dfrac{1}{2}.(180^\circ  - 120^\circ ) = 30^\circ \)

Hay \(y = 30^\circ \).

Vậy \(x = 60^\circ \); \(y = 30^\circ \). 

Từ đồ thị hàm số ta có phương trình tổng quát

\(y = x \Leftrightarrow {d_1}:x - y = 0\), \(y = 2x + 1 \Leftrightarrow 2x - y + 1 = 0\)

Từ đó ta có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}}  = \left( {1; - 1} \right),\overrightarrow {{n_2}}  = \left( {2; - 1} \right)\)

\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + ( - 1).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{3\sqrt {10} }}{{10}} \Rightarrow \left( {{d_1},{d_2}} \right) \approx 18^\circ 26'\)

Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng \(18^\circ 26'\)

Lô

Lời giải:

a.

Đồ thị màu xanh lá: $y=\frac{1}{2}x+1$

Đồ thị màu xanh dương: $y=-x-1$

b.

Ta có:

$\tan \alpha=\frac{1}{2}\Rightarrow \alpha=26,57^0$

$\tan \beta = -1\Rightarrow \beta=135^0$

\(x=\dfrac{10\pi}{7}=-\dfrac{4\pi}{7}+2\pi\)

Do đó số đo hình học là \(\dfrac{4\pi}{7}\)

\(-2345^0=175^0-7.360^0\)

Do đó số đo hình học là \(175^0\)

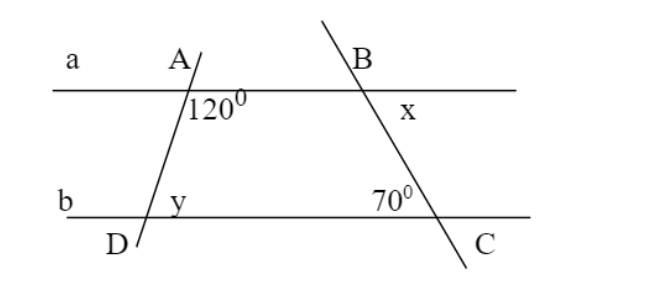
vì a//b nên A+y=180(trong cùng phía

=>y=180-A=180-120=60

vì a//b nên x=C=70(so le trong)

Theo đề ta có:

x.y=24

x/3=y/2

Áp dụng dãy tỉ số bằng nhau ta có:

\(\frac{x}{3}=\frac{y}{2}=\frac{x.y}{3.2}\) 

\(=\frac{24}{6}=4\)

\(\Rightarrow x=3.4=12\)

\(\Rightarrow y=2.4=8\)

Đặt \(k=\frac{x}{3}=\frac{y}{2}\)

Suy ra : \(k^2=\frac{x.y}{3.2}=\frac{24}{6}=4\)

Nên : k = -2;2

+ k = -2 thì \(\frac{x}{3}=-2\Rightarrow x=-6\)

                  \(\frac{y}{2}=-2\Rightarrow x=-4\)

+ k = 2 thì \(\frac{x}{3}=2\Rightarrow x=6\)

                  \(\frac{y}{2}=2\Rightarrow x=4\)

Vậy ......................

Bài 2 :

Vì tam giác abc có số đo các góc a ,b,c lần lượt tỉ lệ là:3:4:5 . 

Nên : \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)

Tổng 3 góc trong 1 tam giác bằng 180^o 

Nên : a + b + c = 180

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}==\frac{180}{12}=15\)

Nên : \(\frac{a}{3}=180\Rightarrow a=60\)

          \(\frac{b}{4}=180\Rightarrow b=45\)

           \(\frac{c}{5}=180\Rightarrow c=36\)

Vậy a = 60 ; b = 45 ; c = 36

cho tỉ lệ thức x/2=y/3 và x.y 24

ko hiêu bài 1