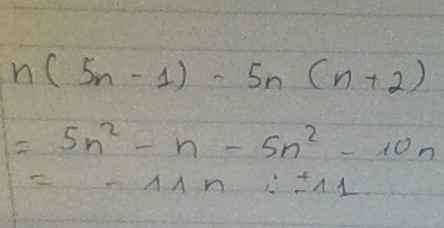Với số nguyên n bất kỳ, biểu thức n(5n-1) - 5n(n+2) luôn chia hết cho bao nhiêu gấp ạ
H24
Những câu hỏi liên quan
Với số nguyên n bất kỳ, biểu thức n(5n-1) - 5n(n+2) luôn chưa hết cho bao nhiêu
Với số nguyên nn bất kỳ, biểu thức n(5n - 2) - 5n(n + 3)n(5n−2)−5n(n+3) luôn chia hết cho bao nhiêu?
Ta có:
\(n\left(5n-2\right)-5n\left(n+3\right)\)
\(=n\left(5n-2\right)-n\left(5n+3\right)\)|
\(=n\left(5n-2-5n-3\right)=-5n\) ; Vì \(n\in Z\)
\(\Rightarrow-5n\in Z\Rightarrow
-5n⋮-5\)
Vậy: .......
#HọcTốt!!
Đúng 0
Bình luận (0)
Với số nguyên n bất kỳ, biểu thức n(4n - 1) - 4n(n + 2) luôn chia hết cho bao nhiêu?
n(4n-1)-4n(n+2)=4n2-n-4n2-8n=-9n
=>n(4n-1)-4n(n+2) luôn chia hết cho 9
Cảm ơn bạn nhoa~
n( 4n - 1 ) - 4n( n + 2 ) = 4n2 - n - 4n2 - 8n = -9n \(⋮\)9
Với số nguyên nn bất kỳ, biểu thức n(3n - 2) - 3n(n + 1)n(3n−2)−3n(n+1) luôn chia hết cho bao nhiêu?
Ta có: n(2n−3)−2n(n+1)n(2n−3)−2n(n+1) = 2n2−3n−2n2−2n2n2−3n−2n2−2n
= −5n−5n
Vì −5⋮5−5⋮5 => -5n ⋮⋮ 5
=> n(2n−3)−2n(n+1)n(2n−3)−2n(n+1) ⋮⋮ 5 với mọi n ∈ Z
Đây nhá bạn
Cảm ơn bạn nha ~
n( 3n - 2 ) - 3n( n + 1 ) = 3n2 - 2n - 3n2 - 3n = -5n \(⋮\)5
Với số nguyên nn bất kỳ, biểu thức n(3n - 2) - 3n(n + 2)n(3n−2)−3n(n+2) luôn chia hết cho bao nhiêu?
n( 3n - 2 ) - 3n( n + 2 )
= 3n2 - 2n - 3n2 - 6n
= -8n luôn chia hết cho ±1 ; ±2 ; ±4 ; ±8
Chứng minh biểu thức
S
n
3
n
+
2
2
+
n
+
1
n
3
−
5
n
+
1
−
2
n
−
1
chia hết cho 120, với n là số nguyên.
Đọc tiếp
Chứng minh biểu thức S = n 3 n + 2 2 + n + 1 n 3 − 5 n + 1 − 2 n − 1 chia hết cho 120, với n là số nguyên.
Ta có:
S = n n 4 + 5 n 3 + 5 n 2 − 5 n − 6 = n [ n 2 − 1 n 2 + 6 + 5 n n 2 − 1 ] = n ( n 2 − 1 ) ( n 2 + 5 n + 6 ) = n ( n − 1 ) ( n + 1 ) ( n + 2 ) ( n + 3 ) = ( n − 1 ) n ( n + 1 ) ( n + 2 ) ( n + 3 )
Ta có S là tích của 5 số nguyên tự nhiên liên tiếp chia hết cho 5! nên chia hết cho 120.
Đúng 0
Bình luận (0)
Với số nguyên nn bất kỳ, biểu thức n(2n - 2) - 2n(n + 3)n(2n−2)−2n(n+3) luôn chia hết cho bao nhiêu?
a 77
b 88
c 1111
d 1010
cho biểu thức A=n^2+5n+10. Chứng minh rằng với mọi số nguyên n thì A ko chia hết cho 25
Tìm số nguyên n để:
a) n3 – 2 chia hết cho n – 2
b) n3 – 3n2 – 3n – 1 chia hết cho n2 + n + 1
c) 5n – 2n chia hết cho 63
giúp vs ạ...
a: \(n^3-2⋮n-2\)
=>\(n^3-8+6⋮n-2\)
=>\(6⋮n-2\)
=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)
b: \(n^3-3n^2-3n-1⋮n^2+n+1\)
=>\(n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)
=>\(3⋮n^2+n+1\)
=>\(n^2+n+1\in\left\{1;-1;3;-3\right\}\)
mà \(n^2+n+1=\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall n\)
nên \(n^2+n+1\in\left\{1;3\right\}\)
=>\(\left[{}\begin{matrix}n^2+n+1=1\\n^2+n+1=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)
Đúng 3
Bình luận (0)