Tính các góc trong của tứ giác !
Gấp !!!!
Tứ giác ABCD có số đo của các góc lập thành một cấp số cộng theo thứ tự A, B, C, D. Biết rằng góc C gấp năm lần góc A. Tính các góc của tứ giác.
Kí hiệu: ∠ : góc
Các góc của tứ giác là ∠A, ∠B, ∠C, ∠D (∠A > 0) tạo thành cấp số cộng:
⇒ ∠B = ∠A + d,
∠C = ∠A + 2d,
∠D = ∠A + 3d.
Theo giả thiết, góc C gấp năm lần góc A nên:
∠C = 5∠A
⇒ ∠A + 2d = 5∠A
⇒ 2d = 4∠A
hay d = 2.∠A
Tổng 4 góc của 1 tứ giác bằng 360º nên ta có:
⇒ ∠A + ∠B + ∠C + ∠D = 360º
⇒ ∠A + ∠A + d + ∠A + 2d + ∠A + 3d = 360º
=> 4∠A +6d = 360º
⇒ 4∠A + 12∠A = 360º ( do d = 2.ºA)
⇒ 16∠A = 360º
⇒ ∠A = 22º30'
⇒ d = 45º.
Vậy ∠A = 22º30' ; ∠B = 67º30'; ∠C = 112º30’; ∠D = 157º30'
Tứ giác ABCD có số đo (độ) của các góc lập thành một cấp số cộng theo thứ tự A, B, C, D. Biết rằng góc C gấp năm lần góc A. Tính các góc của tứ giác ?
Theo giả thiết ta có: A, B, C, D là một cấp số nhân và C = 4A
Theo tính chất của cấp số nhân ta có:
B2 = AC = A.(4A) = 4A2 ⇒ B = 2A
C2 = BD ⇒ (4A)2 = (2A).D ⇒ D = 8A
Mặt khác: A + B + C + D = 3600
⇒ A + 2A + 4A + 8A = 3600
⇒ A = 240 ⇒ B = 480, C = 960, D = 1920.
Cho tam giác ABC, các phân giác trong của hai góc B,C cắt nhau tại I và các phân giác ngoài của hai góc B,C cắt nhau tại J.
a) Tính các góc của tứ giác BICJ theo góc A
b) Áp dụng, tính các góc của tứ giác BICJ khi góc A =70
Cho tứ giác abcd .tính các góc của tứ giác biết 4 góc bằng nhau
Cho tứ giác abcd .tính độ lớn từng góc trong tứ giác nếu độ lớn góc A góc B góc C góc D lần lượt tỷ lệ với 1;2;4;5
1. Xét tứ giác ABCD ta có :
^A + ^B + ^C + ^D = 3600 ( định lí )
mà 4 góc đó bằng nhau
=> ^A = ^B = ^C = ^D = 3600/4 = 900
2. Xét tứ giác ABCD ta có :
^A + ^B + ^C + ^D = 3600 ( định lí ) (1)
mà ^A , ^B , ^C , ^D lần lượt tỉ lệ với 1 ; 2 ; 4 ; 5
=> \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}\)(2)
Từ (1) và (2) => Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+4+5}=\frac{360^0}{12}=30^0\)
=> ^A = 300
^B = 300.2 = 600
^C = 300.4 = 1200
^D = 300.5 = 1500
Xét tứ giác ABCD có các góc bằng nhau
=> \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}\)
Mà \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\left(dl\right)\)
\(\Leftrightarrow4\widehat{A}=360^o\Leftrightarrow\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\)
Bài 2:
Xét tứ giác ABCD
=> \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Vì các góc tứ giác ABCD lần lượt tỉ lệ với 1:2:4:5
\(\Rightarrow\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}\)VÀ \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Theo tính chất dãy tỉ số bằng nhau
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{4}=\frac{\widehat{D}}{5}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+4+5}=\frac{360^o}{12}=30^o\)
Do đó
\(\frac{\widehat{A}}{1}=30^o\Leftrightarrow\widehat{A}=30^o\)
\(\frac{\widehat{B}}{2}=30^o\Leftrightarrow\widehat{B}=60^o\)
\(\frac{\widehat{C}}{4}=30^o\Leftrightarrow\widehat{C}=120^o\)
\(\frac{\widehat{C}}{5}=30^o\Leftrightarrow\widehat{C}=150^o\)
Vậy.........
a,
1 tứ giác có tổng 4 góc là 360 độ nên 1 góc có :
360 : 4 = 90 độ
b,
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{4}=\frac{d}{5}=\frac{a+b+c+d}{1+2+4+5}=\frac{360}{12}=30\)
\(\frac{a}{1}=30\Rightarrow a=30\)
\(\frac{b}{2}=30\Rightarrow b=60\)
\(\frac{c}{4}=30\Rightarrow c=120\)
\(\frac{d}{5}=30\Rightarrow d=150\)
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính các góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
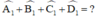
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
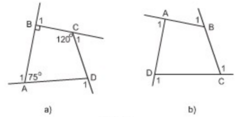
a) + Góc ngoài tại A là góc A1:
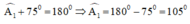
+ Góc ngoài tại B là góc B1:
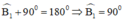
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
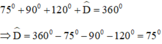
Lại có:
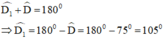
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
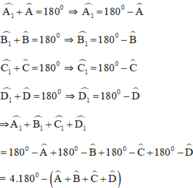
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
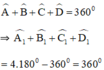
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.
Tứ giác ABCD có góc A - góc C = 60 độ các tia phân giác của các góc B và góc D cắt nhau tại I trong tứ giác . Tính góc BID
Cho tứ giác ABCD biết số đo của các góc A, B, C, D tỉ lệ thuận với 1,2,3,4.
Tính số đo của các góc trong tứ giác ABCD.
Tứ giác ABCD có số đo bốn góc A, B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo góc C gấp 5 lần số đo góc A. Tính số đo các góc của tứ giác ABCD theo đơn vị độ.
Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B = A + d; C = A + 2d; D = A + 3d.
Mặt khác: A + B + C + D = 360°
⇔ A + A + d + A + 2d + A + 3d = 360°
⇔ 4A + 6d = 360°
⇔ 2A + 3d = 180°
Ta lại có: A + 2d = 5A ⇔ d = 2A
⇒ 8A = 180°
⇒ A = 22,5° và d = 45°
⇒ B = 67,5°, C = 112,5°, D = 157,5°.
tìm số đo các góc chưa bt của tứ giác trong từng trường hợp sau:
a) tứ giác có các góc 800, 700 và 2 góc còn lại góc này gấp 2 lần góc kia
b) tứ giác có số đo góc lần lượt tỉ lệ vs 1:2:4:5
a) Gọi A = 80°
B = 70°
D = 2C
=> C+D = 360 - 70 - 80 = 210
=> 2C + C = 210°
=> 3C = 210°
=> C = 70°
=> D = 70 × 2 = 140°
b) Ta có : A = B/2=C/4 = D/5
Áp dụng tính chất dãy tỉ số bằng nhau ta có
=> A = 30°
=> B = 60°
=> C = 120°
=> D = 150°
Bài 10. Cho tứ giác , biết . Tính các góc của tứ giác .
Bài 11. Cho tứ giác , biết . Tính các góc của tứ giác
.
Bài 12. Cho tứ giác có . Tính góc
Bài 13. Cho tứ giác biết + = 2000, + = 1800; + = 1200. Tính số đo các góc
EFGH G E 10 , F E 30 , H 2G o o EFGH
MNPQ P Q 5 , M Q 45 , N 2Q 40 o o o
MNPQ
ABCD A 70 , B 80 , C D 20 o o o C, D.
ABCD B C B D C D
tor.com
Bài 14:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{3}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{7}=\dfrac{360^0}{15}=24^0\)
Do đó: \(\widehat{A}=24^0;\widehat{B}=72^0;\widehat{C}=96^0;\widehat{F}=168^0\)