khai triển các biểu thức sau
\(2.\left(\dfrac{1}{2}x^2+y\right)\left(x^2-2y\right)\)
khai triển các biểu thức sau:
\(a.\left(2x+3y\right)^2\)
\(b.2\left(\dfrac{1}{2}x^2+y\right)\left(x^2-2y\right)\)
\(c.\left(x+y+z\right)^2\)
a. (2x+3y)2= (2x)2+2.2x.3y+(3y)2
=4x2+12xy+9y2
b. 2(\(\dfrac{1}{2}\)x2+y)(x2-2y)
=(x2+2y)(x2-2y)
=x4-4y2
c, (x+y+z)2= [(x+y)+z]2
=(x+y)2+2(x+y)z+z2
=x2+2xy+y2+2xz+2yz+z2
=x2+y2+z2+2xy+2yz+2xz
Khai triển các biểu thức sau
a) \({\left( {x - 2} \right)^4}\)
b) \({\left( {x + 2y} \right)^5}\)
a) \({\left( {x - 2} \right)^4}\)
\(\begin{array}{l} = {x^4} + 4{x^3}.\left( { - 2} \right) + 6{x^2}.{\left( { - 2} \right)^2} + 4x{\left( { - 2} \right)^3} + {\left( { - 2} \right)^4}\\ = {x^4} - 8{x^3} + 24{x^2} - 32x + 16\end{array}\)
b) \({\left( {x + 2y} \right)^5}\)
\(\begin{array}{l} = {x^5} + 5.{x^4}.\left( {2y} \right) + 10.{x^3}.{\left( {2y} \right)^2} + 10.{x^2}.{\left( {2y} \right)^3} + 5.x.{\left( {2y} \right)^4} + 1.{\left( {2y} \right)^5}\\ = {x^5} + 10{x^4}y + 40{x^3}{y^3} + 80{x^2}{y^3} + 80x{y^4} + 32{y^5}\end{array}\)
Khai triển các biểu thức sau:
\(\begin{array}{l}a){\left( {5{\rm{x}} - y} \right)^2}\\b){\left( {\frac{1}{2}x + 2y} \right)^3}\end{array}\)
a) Khai triển biểu thức \({\left( {5{\rm{x}} - y} \right)^2}\)
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
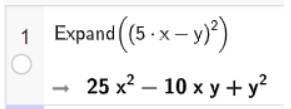
Vậy \({\left( {5{\rm{x}} - y} \right)^2} = 25{{\rm{x}}^2} - 10{\rm{x}}y + {y^2}\)
b) Khai triển biểu thức: \({\left( {\frac{1}{3}x + 2y} \right)^3}\)
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
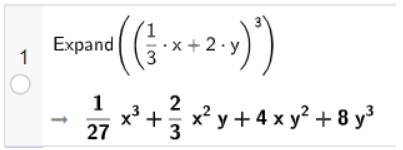
Vậy \({\left( {\frac{1}{3}x + 2y} \right)^3} = \frac{1}{{27}}{x^3} + \frac{2}{3}{x^2}y + 4{\rm{x}}{y^2} + 8{y^3}\)
Rút gọn các biểu thức sau:
a/ \(\left(x-2y^{ }\right)^2+\left(x-\dfrac{1}{2}y\right)\left(x+\dfrac{1}{2}y\right)\)
b/ \(\left(x-2\right)^2+\left(x+3\right)^2-2\left(x-1\right)\left(x+1\right)\)
a: \(\left(x-2y\right)^2+\left(x-\dfrac{1}{2}y\right)\left(x+\dfrac{1}{2}y\right)\)
\(=x^2-4xy+4y^2+x^2-\dfrac{1}{4}y^2\)
\(=2x^2-4xy+\dfrac{15}{4}y^2\)
b: \(\left(x-2\right)^2+\left(x+3\right)^2-2\left(x-1\right)\left(x+1\right)\)
\(=x^2-4x+4+x^2+6x+9-2\left(x^2-1\right)\)
\(=2x^2+2x+13-2x^2+2\)
=2x+15
a) \(=x^2-4xy+4y^2+x^2-\dfrac{1}{4}y^2=2x^2-4xy+\dfrac{15}{4}y^2\)
b) \(=x^2-4x+4+x^2+6x+9-2x^2+2\)
\(=2x+15\)
a; \(\left(x-2y\right)^2+\left(x-\dfrac{1}{2}y\right)\left(x+\dfrac{1}{2}y\right)\)
= \(x^2-4xy+4y^2+x^2-\dfrac{1}{4}y^2\)
= \(2x^2-4xy+\dfrac{15}{4}y^2\)
b; \(\left(x-2\right)^2+\left(x+3\right)^2-2\left(x-1\right)\left(x+1\right)\)
= \(x^2-4x+4+x^2+6x+9-2x^2+2\)
= \(2x+15\)
Áp dụng hằng đẳng thức, khai triển các biểu thức sau:
a, \(\left(2x+y+3\right)^2\)
b, \(\left(x-2y+1\right)^2\)
c, \(\left(x^2-2xy^2-3\right)^2\)
\(a,\left(2x+y+3\right)^2=4x^2+y^2+9+4xy+12x+6y\)
\(b,\left(x-2y+1\right)^2=x^2+4y^2+1-4xy+2x-4y\)
\(c,\left(x^2-2xy^2-3\right)^2=x^4+2x^2y^4+9-4x^3y^2-6x^2+12xy^2\)
Viết các biểu thức sau thành đa thức:
a) \(\left( {3x - 5} \right)\left( {3x + 5} \right)\) b) \(\left( {x - 2y} \right)\left( {x + 2y} \right)\) c) \(\left( { - x - \dfrac{1}{2}y} \right)\left( { - x + \dfrac{1}{2}y} \right)\)
a) \(\left(3x-5\right)\left(3x+5\right)\)
\(=\left(3x\right)^2-5^2\)
\(=9x^2-25\)
b) \(\left(x-2y\right)\left(x+2y\right)\)
\(=x^2-\left(2y\right)^2\)
\(=x^2-4y^2\)
c) \(\left(-x-\dfrac{1}{2}y\right)\left(-x+\dfrac{1}{2}y\right)\)
\(=\left(-x\right)^2-\left(\dfrac{1}{2}y\right)^2\)
\(=x^2-\dfrac{1}{4}y^2\)
`a, (3x-5)(3x+5) = 9x^2 - 25`
`b, (x-2y)(x+2y) = x^2 -4y^2`
`c, (-x-1/2y)(-x+1/2y) = x^2 - 1/4y^2`
Khai triển biểu thức :
1, \(\left(2x-3y\right)^3\)
2, \(\left(2x+\dfrac{9}{2}\right)^3\)
3, \(\left(x+2y\right)^3+\left(x-2y\right)^3\)
4, \(\left(2x+1\right)^3-\left(x-1\right)^3-7\cdot\left(x+1\right)^3\)
a, \(\left(2x-3y\right)^3=8x^3-36x^2y+54xy^2-27y^3\)
b, \(\left(2x+\dfrac{9}{2}\right)^3=8x^3-54x^2+121,5x-91,125\)
c, \(\left(x+2y\right)^3+\left(x-2y\right)^3=x^3+6x^2y+12xy^2+8y^3+x^3-6x^2y+12xy^2-8y^3\)
\(=2x^3+24xy^3\)
d, \(\left(2x+1\right)^3-\left(x-1\right)^3-7\left(x+1\right)^3\)
\(=8x^3+12x^2+6x+1-\left(x^3-3x^2+3x-1\right)-7\left(x^3+3x^2+3x+1\right)\)
\(=8x^3+12x^2+6x+1-x^3+3x^2-3x+1-7x^3-21x^2-21x-7\)
\(=-6x^2-18x-5\)
Chúc bạn học tốt!!!
CHo x,y là các số thực không âm Tím max của biểu thức
\(P=\dfrac{\left(x^2-y^2\right)\left(1-x^2y^2\right)}{\left(1+x^2\right)^2\left(1+y^2\right)^2}\)
\(\left(x^2;y^2\right)=\left(a;b\right)\Rightarrow P=\dfrac{\left(a-b\right)\left(1-ab\right)}{\left(1+a\right)^2\left(1+b\right)^2}\)
Ta có:
\(\left(a+b\right)\left(1+ab\right)-\left(a-b\right)\left(1-ab\right)=2b\left(a^2+1\right)\ge0;\forall a;b\ge0\)
\(\Rightarrow\left(a+b\right)\left(1+ab\right)\ge\left(a-b\right)\left(1-ab\right)\)
\(\Rightarrow P\le\dfrac{\left(a+b\right)\left(1+ab\right)}{\left(1+a\right)^2\left(1+b\right)^2}\le\dfrac{\left(a+b+1+ab\right)^2}{4\left(1+a\right)^2\left(1+b\right)^2}=\dfrac{1}{4}\)
\(P_{max}=\dfrac{1}{4}\) khi \(\left(a;b\right)=\left(1;0\right)\) hay \(\left(x;y\right)=\left(1;0\right)\)
\(P=\dfrac{\left[\left(x-y\right)\left(1+xy\right)\right]\left[\left(x+y\right)\left(1-xy\right)\right]}{\left(1+x^2\right)^2\left(1+y^2\right)^2}\)
Áp dụng BĐT Cosi ta có:
\(\left(x-y\right)\left(1+xy\right)\le\dfrac{\left(x-y\right)^2+\left(1+xy\right)^2}{2}=\dfrac{\left(1+x^2\right)\left(1+y^2\right)}{2}\\ \left(x+y\right)\left(1-xy\right)\le\dfrac{\left(x+y\right)^2+\left(1-xy\right)^2}{2}=\dfrac{\left(1+x^2\right)\left(1+y^2\right)}{2}\)
\(\to P\le\dfrac{\left(1+x^2\right)^2\left(1+y^2\right)^2}{4\left(1+x^2\right)^2\left(1+y^2\right)^2}=\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow\left(x;y\right)=\left(1;0\right)\)
Dùng hằng đẳng thức để khai triển và thu gọn :
a,\(\left(-3xy^4+\dfrac{1}{2}x^2y^2\right)^3\)
b,\(\left(-\dfrac{1}{3}ab^2-2a^3b\right)^3\)