Tìm x
a) 2x + 69 . 2 = 69 . 4
b) 2x - 12 - x = 0
c) ( x + 1 ) + ( x + 2 ) + ... + ( x + 10 ) = 165
1. Tìm X <- N.
a) 3 : ( 2x + 1 ) + 69 = 72
b) 165 - ( 35 : x + 3 ) . 19 = 13
c) { [ ( 2x + 14 ) : 4 - 3 ] : 2 } - 1 = 0
d) 10 - { [ ( x : 3 + 17 ) : 10 + 316 ] : 16 } = 5
a)\(3:\left(2x+1\right)=72-69\)
\(3:\left(2x+1\right)=3\)
\(2x+1=3:3\)
\(2x+1=1\)
\(2x=1-1\)
\(2x=0\)
\(x=0:2\)
\(x=0\)
các bài còn lại giống như câu a nha nếu ko biết thì comment lại minhf sẽ giải cho . Nhớ k cho mình nha
(35:x+3).19=165-13=152
35:x+3=152:19=8
35:x=8-3=5
x=35:5=7
tìm STN x
2x + 69 . 2 = 69 . 4
2x - 12 - x = 0
(x-7) . (2x - 8) = 0
2x+69.2=69.4
2x+138=276
2x = 276-138
2x = 138
x = 138:2
x = 69
2x-12-x = 0
<=> 2x-x-12 =0
(2x-x)-12=0
=> x-12=0
x = 0+12
x =12
(x-7)(2x-8)=0
\(\Rightarrow\hept{\begin{cases}x-7=0\\2x-8=0\end{cases}}\Rightarrow\hept{\begin{cases}x=7\\x=4\end{cases}}\)
Vậy ...
a, 2X+69.2=69.4
2X+138=276
2X=276-138=138
X=138:2=69
b,2X-12-x=0
2X-X=12-0
x=12
mik chi biet vay thoi con cau cuoi mik chiu
2x+69.2=69.4
2x=69.4-69.2
2x=69.(4-2)
2x=69.2
x=69.2/2
x=69
2x-12-x=0
2x-x=0+12
x=12
(x-7).(2x-8)=0
ta có hai trường hợp:
trường hợp 1: x-7=0
x=7
trường hợp 2:
2x-8=0
2x=8
x=4
bạn cố gắng hiểu nha. mình làm hơi tắt.
Giải các bất phương trình và biểu diễn nghiệm trên trục số:
a ) x + 2 2 - 10 ≥ x + 3 x + 2 - 4 b ) x - 2 18 - 2 x + 5 12 > x + 6 9 - x - 3 6
a)
⇔ x2 + 6x + 9 – 10 ≥ x2 + 3x + 2x + 6 – 4
⇔ x2 – x2 + 6x – 3x – 2x ≥ –9 + 10 + 6 – 4
⇔ x ≥ 3
Tập nghiệm: S = {x | x ≥ 3}.
Biểu diễn trên trục số:
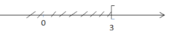
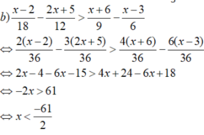
Vậy tập nghiệm của bất phương trình là
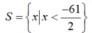
Tìm x:
a) x(x-1)+x=4
b) 3x(x-5)-2x+10=0
c) 5x2-3x-2=0
d) x4-11x2+18=0
a) \(x^2-x+x=4\)
\(x^2=4\)
\(x=\pm2\)
b) \(3x\left(x-5\right)-2\left(x-5\right)=0\)
\(\left(x-5\right)\left(3x-2\right)=0\)
\(\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\end{matrix}\right.\)
c) Ta có: \(a+b+c=5-3-2=0\)
\(\left[{}\begin{matrix}x=1\\x=\dfrac{c}{a}=\dfrac{-2}{5}\end{matrix}\right.\)
d) Đặt \(x^2=t\left(t\ge0\right)\) . Lúc đó phương trình trở thành :
\(t^2-11t+18=0\)
\(\left[{}\begin{matrix}t=9\left(tmđk\right)\\t=2\left(tmđk\right)\end{matrix}\right.\)
\(t=9\rightarrow x^2=9\rightarrow x=\pm3\)
\(t=2\rightarrow x^2=2\rightarrow x=\pm\sqrt{2}\)
Tìm x
2x-12=18
317-(x-69)=286
10+2x=2^3×3^2
Giúp mình nha thanks
2x - 12 = 18................................
2x = 30 ........................................
x = 15.....................................
2x - 12 = 18................................
2x = 30 ........................................
x = 15.....................................
Tìm x: ( mình cần gấp )
a) x(x-1)+x=4
b) 3x(x-5)-2x+10=0
c) 5x2-3x-2=0
d) x4-11x2+18=0
a:Ta có: \(x\left(x-1\right)+x=4\)
\(\Leftrightarrow x^2-x+x=4\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
b: Ta có: \(3x\left(x-5\right)-2x+10=0\)
\(\Leftrightarrow\left(x-5\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\end{matrix}\right.\)
c: Ta có: \(5x^2-3x-2=0\)
\(\Leftrightarrow5x^2-5x+2x-2=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2}{5}\end{matrix}\right.\)
d: Ta có: \(x^4-11x^2+18=0\)
\(\Leftrightarrow x^4-9x^2-2x^2+18=0\)
\(\Leftrightarrow x^2\left(x^2-9\right)-2\left(x^2-9\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
a) x(x-1)+x=4
⇔x2=4⇔\(x=\pm2\)
b)3x(x-5)-2x+10=0
⇔3x(x-5)-2(x-5)=0
⇔(x-5)(3x-1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{3}\end{matrix}\right.\)
c)5x2-3x-2=0
⇔ 5x(x-1)+2(x-1)=0
⇔ (x-1)(5x+2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2}{5}\end{matrix}\right.\)
d)x4-11x2+18=0
⇔ x2(x2-2)-9(x2-2)=0
⇔ (x2-2)(x2-9)=0
\(\Leftrightarrow\left[{}\begin{matrix}x^2=2\\x^2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x=\pm3\end{matrix}\right.\)
tìm x
a, (2x - 3)\(^2\) = |3 - 2x|
b, (x - 1)\(^2\) + (2x - 1)\(^2\) - 0
c, x - 2\(\sqrt{x}\) = 0
d, (x - 1)\(^2\) + 1/7 = 0
a: \(\left(2x-3\right)^2=\left|3-2x\right|\)
=>\(\left\{{}\begin{matrix}\left|2x-3\right|>=0\\\left(2x-3\right)^2=\left(2x-3\right)\end{matrix}\right.\Leftrightarrow\left(2x-3\right)^2-\left(2x-3\right)=0\)
=>\(\left(2x-3\right)\left(2x-3-1\right)=0\)
=>\(\left(2x-3\right)\left(2x-4\right)=0\)
=>\(\left[{}\begin{matrix}2x-3=0\\2x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\end{matrix}\right.\)
b: \(\left(x-1\right)^2+\left(2x-1\right)^2=0\)
=>\(x^2-2x+1+4x^2-4x+1=0\)
=>\(5x^2-6x+2=0\)
\(\Delta=\left(-6\right)^2-4\cdot5\cdot2=36-20\cdot2=-4< 0\)
=>Phương trình vô nghiệm
c: ĐKXĐ: x>=0
\(x-2\sqrt{x}=0\)
=>\(\sqrt{x}\cdot\sqrt{x}-2\cdot\sqrt{x}=0\)
=>\(\sqrt{x}\left(\sqrt{x}-2\right)=0\)
=>\(\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
d: \(\left(x-1\right)^2+\dfrac{1}{7}=0\)
mà \(\left(x-1\right)^2+\dfrac{1}{7}>=\dfrac{1}{7}>0\forall x\)
nên \(x\in\varnothing\)
TÌM X
a. 3.(x^2-x+2)-x.(2+3x)=0
b. (x-1)^2 + (x-1)(x+2)=0
c. 2x^3 +3x^2+2x+3=0
d. 2x^2+x=6
\(a,\Rightarrow3x^2-3x+6-2x-3x^2=0\\ \Rightarrow-5x=-6\Rightarrow x=\dfrac{6}{5}\\ b,\Rightarrow\left(x-1\right)\left(x-1+x+2\right)=0\\ \Rightarrow\left(x-2\right)\left(2x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{1}{2}\end{matrix}\right.\\ c,\Rightarrow x^2\left(2x+3\right)+\left(2x+3\right)=0\\ \Rightarrow\left(x^2+1\right)\left(2x+3\right)=0\Rightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\2x+3=0\end{matrix}\right.\\ \Rightarrow x=-\dfrac{3}{2}\\ d,\Rightarrow2x^2+x-6=0\\ \Rightarrow2x^2+4x-3x-6=0\\ \Rightarrow2x\left(x+2\right)-3\left(x+2\right)=0\\ \Rightarrow\left(2x-3\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\)
Tìm x
a, 4x\(^2\)-1-x(2x+1)=0
b, x\(^2\)-7x+12=0
c, x\(^2\)-8x+6=0
\(a,\Rightarrow\left(2x-1\right)\left(2x+1\right)-x\left(2x+1\right)=0\\ \Rightarrow\left(2x+1\right)\left(2x-1-x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\\ b,\Rightarrow\left(x-3\right)\left(x-4\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\\ c,\Rightarrow\left(x^2-8x+16\right)-10=0\\ \Rightarrow\left(x-4\right)^2-10=0\\ \Rightarrow\left(x-4-\sqrt{10}\right)\left(x-4+\sqrt{10}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4+\sqrt{10}\\x=4-\sqrt{10}\end{matrix}\right.\)