a)
⇔ x2 + 6x + 9 – 10 ≥ x2 + 3x + 2x + 6 – 4
⇔ x2 – x2 + 6x – 3x – 2x ≥ –9 + 10 + 6 – 4
⇔ x ≥ 3
Tập nghiệm: S = {x | x ≥ 3}.
Biểu diễn trên trục số:
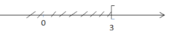
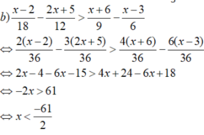
Vậy tập nghiệm của bất phương trình là
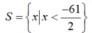
a)
⇔ x2 + 6x + 9 – 10 ≥ x2 + 3x + 2x + 6 – 4
⇔ x2 – x2 + 6x – 3x – 2x ≥ –9 + 10 + 6 – 4
⇔ x ≥ 3
Tập nghiệm: S = {x | x ≥ 3}.
Biểu diễn trên trục số:
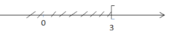
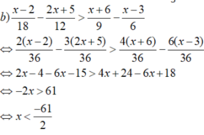
Vậy tập nghiệm của bất phương trình là
`1)` Giải các pt `a)(x+2)/(x-3)+x/(x+2)=(x^{2}+6)/(x^{2}-x-6)` `b)(x+1)^{2}+|x-1|=x^{2}+4` `2)` Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số `1-(x-1)/3<(x+3)/3-(x-2)/2`
giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a, 3x+6>0
b, 10-2x≥-4
c, \(\dfrac{3x-2}{-3}>\dfrac{1-x}{5}\)
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số: a, 5x+10<=0. b,2x+4>3x+3. C, 2x+4=>2(x+1)-3. d, 2(x+1)<5(x-2)-3x.
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 4x + 6 <= 2x - 2
b) 3x + 15 < 0
c) 3x - 3 > x + 5
d) x - 4 >= - 2x + 5
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số
x - 2/4 - 2/3 ≥ 5x - 9 / 12
giải phương trình sau
1/ x +2 - 5/ x-2 = 2x-3 / x2
a) giải phương trình: 8x-3=5x+12
b) giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{8-11x}{4}\)< 13
c) Chứng minh rằng: (\(\dfrac{x}{x^2-36}\)- \(\dfrac{x-6}{x^2+6x}\)): \(\dfrac{2x-6}{x^2+6x}\)+ \(\dfrac{x}{6-x}\)= 1
giải các bất phương sau và biểu diễn tập nghiệm trên trục số
a)\(\dfrac{x-1}{6}-\dfrac{x+2}{4}< \dfrac{x+3}{2}-\dfrac{x-5}{3}\)
b)\(\dfrac{x-1}{x-2}>\dfrac{x-3}{x-4}\)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) ( 2 x + 3 ) ( 2 x − 1 ) < ( 2 x − 5 ) 2
b) ( x − 1 ) ( x + 2 ) < ( x − 1 ) 2 + 3
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a.3x-5 >15-x b.3(x-2).(x+2)<3x^2+x
c.(2x+1)^2+(1-x).3x<hoặc=(x+2)^2
d.5x-20/3 - 2x^2+x/2 > x.(1-3x)/3 -5x/4
e.4-2x <hoặc= 3x-6
f.(x+4).(5x-1)>5x^2+16x+2
g)x.(2x-1)-8<5-2x(1-x)
h)3x-1/4 - 3.(x-2)/8 - 1>5-3x/2
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a.3x-5 >15-x b.3(x-2).(x+2)<3x^2+x
c.(2x+1)^2+(1-x).3x<hoặc=(x+2)^2
d.5x-20/3 - 2x^2+x/2 > x.(1-3x)/3 -5x/4
e.4-2x <hoặc= 3x-6
f.(x+4).(5x-1)>5x^2+16x+2
g)x.(2x-1)-8<5-2x(1-x)
h)3x-1/4 - 3.(x-2)/8 - 1>5-3x/2