cho hình thang ABCD có AB song song với CD kẻ đường cao AH,BK chứng minh BH=CK
cho hình thang cân ABCD có AB song song với C (AB<CD) kể các đường cao AH ,BK ,chứng minh DH=CK
mấy cái câu kiểu này có hình thì hay bt mấy nhỉ
Xét tam giác ABC và tam giác BKC có :
góc AHD = góc AKC = 90 độ ( gt )
AD = BC ( gt )
góc D = góc C ( gt )
=> tam giác ABC = tam giác BKC ( ch - gn )
=> DH = CK
Cho hình thang cân ABCD(AB song song CD AB phải nhỏ hơn CD)các đường cao AH,BK a,Tứ giác ABCH là hình gì?vì sao? b,Chứng minh BH bằng CK c,Gọi E là điểm đối xứng với D qua H, chứng minh tứ giác ABCE là hình bình hành
a: Xét tứ giác ABCH có
AB//CH
góc AHC=90 độ
Do đó: ABCH là hình thang vuông
b: Sửa đề; DH=CK
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
Do đo: ΔAHD=ΔBKC
=>DH=CK
c: Xét ΔAED có
AH vừa là đường cao, vừa là trung tuyến
nên ΔAED cân tại A
=>góc AED=góc ADE=góc BCD
=>AE//BC
mà AB//CE
nên ABCE là hình bình hành
Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng DH = CK.

Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
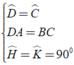
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)
Hình thang cân ABCD có AB //CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DH = CK
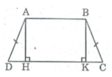
Xét hai tam giác vuông AHD và BKC:
∠ (AHD) = ∠ (BKC) = 90 0
AD = BC (tính chất hình thang cân)
∠ C = ∠ D (gt)
Suy ra: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
⇒ HD = KC
Bài 8: Hình thang cân ABCD có AB // CD, AB < CD. Kẻ đường cao AH, BK. Chứng minh DH = CK.
Xét hai tam giác vuông AHD và BKC:
ˆAHD=ˆBKC=90 độ
AD=BC (tính chất hình thang cân)
ˆC=ˆD (gt)
Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
=> đpcm
Cho hình thang cân ABCD có AB // CD, AB < CD. Kẻ đường cao AH, BK. Chứng minh rằng : DH = CK.
Xét ΔAHD và ΔBKC có:
\(\widehat{AHD}=\widehat{AKC}=90\left(gt\right)\)
AD=BC(gt)
\(\widehat{D}=\widehat{C}\left(gt\right)\)
=>ΔAHD=ΔBKC (cạnh huyền-góc nhọn)
=>DH=CK
Cho hình thang cân ABCD (AB song song với CD) có AB = 7cm, BC = CD= 13cm. Kẻ các đường cao AK và BH
a) Chứng minh rằng CH=DK và AB = HK
b) Tính độ dài BH và diện tích hình thang ABCD
a: Xét ΔAKD vuông tại K và ΔBHC vuông tại H có
AD=BC
góc D=góc C
=>ΔAKD=ΔBHC
=>CH=DK
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AB=HK
b: KH=AB=7cm
=>DK+HC=13-7=6cm
=>DK=HC=6/2=3cm
\(BH=\sqrt{13^2-3^2}=\sqrt{160}=4\sqrt{10}\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}\cdot BH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\sqrt{10}\left(7+13\right)=40\sqrt{10}\left(cm^2\right)\)
cho hình thang cân ABCD(AB//CD, AB<CD) kẻ đường cao AH,BK của hình thang. chứng minh rằng DH=CK
hình thang cân ABCD có AB song song vớiCD,AB<CD.kẻ các đường cao AH,BK
Chứng minh rằng DH=CK
Xét \(\Delta ABC\)và \(\Delta BKC\)có:
\(\widehat{AHD}=\widehat{AKC}=90\)gt
\(AD=BC\)gt
\(\widehat{D}=\widehat{C}\)gt
\(\Rightarrow\Delta AHD=\Delta BKC\)cạnh huyền-góc nhọn
\(\Rightarrow DH=CK\)