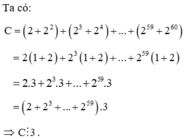Chứng minh rằng : A = 2 + 22 + 23 + 24 + .... + 259 + 260 chia het cho 3
LP
Những câu hỏi liên quan
chung minh tong sau chia het cho 7 A=21+22+23+24+...+259+260
c. 55 - 7 . ( x + 3) = 6
d. (-14) - x + (- 15) = - 10
A = 2 + 22 + 23 + 24 + ... + 259 + 260
Chứng Minh Rằng: A chia hết cho 21
Các bạn giải rõ ra choa mik nhed :)))))
c) \(55-7.\left(x+3\right)=6\)
\(7.\left(x+3\right)=55-6\)
\(7.\left(x+3\right)=49\)
\(x+3=49:7\)
\(x+3=7\)
\(x=7-3\)
\(x=4\)
d) \(-14-x+\left(-15\right)=-10\)
\(-29-x=-10\)
\(x=-29+10\)
\(x=-19\)
-----------------------------
Số số hạng của A:
\(60-1+1=60\) (số)
Do \(60⋮6\) nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 6 số hạng như sau:
\(A=\left(2+2^2+2^3+2^4+2^5+2^6\right)+\left(2^7+2^8+2^9+2^{10}+2^{11}+2^{12}\right)+...+\left(2^{55}+2^{56}+2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2.\left(1+2+2^2+2^3+2^4+2^5\right)+2^7.\left(1+2+2^2+2^3+2^4+2^5\right)+...+2^{55}.\left(1+2+2^2+2^3+2^4+2^5\right)\)
\(=2.63+2^7.63+...+2^{55}.63\)
\(=63.\left(2+2^7+...+2^{55}\right)\)
\(=21.3.\left(2+2^7+...+2^{55}\right)⋮21\)
Vậy \(A⋮21\)
Đúng 2
Bình luận (0)
55-7(x+3)=6
7(x+3)=55-6=49
(x+3)=49:7=7
x=7-3=4
(-14)-x + (-15)=-10
(-14)-x=-10-15=-25
x =-14-25=-39
A chia hết 31 chứ
Đúng 0
Bình luận (0)
Cho đề bài: A = 2 + 22+23+24+ ... + 259+ 260.
a) Tính A
b ) Chứng minh A chia hết cho 21
Please help meee
a: \(2A=2^2+2^3+...+2^{61}\)
=>A=2^61-2
b: \(A=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{55}+2^{58}\right)\) chia hết cho 7(1)
\(A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)=3\left(2+2^3+...+2^{59}\right)⋮3\left(2\right)\)
Từ (1), (2) suy ra A chia hết cho 21
Đúng 2
Bình luận (0)
Câu 5: Chứng minh tổng sau chia hết cho 7.
A = 21 + 22 + 23 + 24 +...+ 259 + 260
Đề sai, viết lại thành:
A= 21+22+23+24+...+259+260
Giải:
A=21+22+23+...............+259+260
A=(21+22+23)+...............+(258+259+260)
A=2.(1+2+22)+............+258.(1+2+22)
A=2.7+.......................+258.7
A=(2+24+..............+258).7 ⋮ 7(đpcm)
Đúng 1
Bình luận (1)
Câu 6: Chứng tỏ A = 2 + 22 + 23 + 24….+ 259 + 260
a. Chia hết cho 3;
b. Chia hết cho 7.
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
A= (2+22+23)+...+(258+259+260)
A=2.(1+2+22)+...+258.(1+2+22)
A=2.7+...+258.7
A=7.(2+...+258)
Vì 7 chia hết cho 7 =>7.(2+...+258) chia hết cho 7
CHIA HẾT CHO 3 :
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
B=2+22+23+24+..............+259+260 b chia hết cho 2,3,7,15
\(B=2\left(1+2+2^2+...+2^{58}+2^{59}\right)⋮2\)
\(B=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{59}\right)⋮3\)
\(B=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{58}\right)⋮7\)
\(B=2\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{57}\right)⋮15\)
Đúng 2
Bình luận (1)
Cho: A = 2 + 22 + 23 + 24 +....+ 260
Chứng minh rằng: A⋮3; A⋮5;A⋮7
Thanks!
\(A=2+2^2+2^3+2^4+...+2^{60}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{59}+2^{60}\right)\)
\(A=6+2^2.\left(2+2^2\right)+...+2^{58}.\left(2+2^2\right)\)
\(A=6+2^2.6+...+2^{58}.6\)
\(A=6.\left(1+2^2+...+2^{58}\right)\)
Vì \(6⋮3\) nên \(6.\left(1+2^2+...+2^{58}\right)⋮3\)
Vậy \(A⋮3\)
_________________
\(A=2+2^2+2^3+2^4+...+2^{60}\)
\(A=\left(2+2^2+2^3+2^4\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(A=30+...+2^{56}.\left(2+2^2+2^3+2^4\right)\)
\(A=30+...+2^{56}.30\)
\(A=30.\left(1+...+2^{56}\right)\)
Vì \(30⋮5\) nên \(30.\left(1+...+2^{56}\right)⋮5\)
Vậy \(A⋮5\)
_________________
\(A=2+2^2+2^3+2^4+...+2^{60}\)
\(A=\left(2+2^2+2^3\right)+...+\left(2^{58}+2^{59}+2^{60}\right)\)
\(A=14+...+2^{57}.\left(2+2^2+2^3\right)\)
\(A=14+...+2^{57}.14\)
\(A=14.\left(1+...+2^{57}\right)\)
Vì \(14⋮7\) nên \(14.\left(1+...+2^{57}\right)⋮7\)
Vậy \(A⋮7\)
\(#WendyDang\)
Đúng 1
Bình luận (0)
Chứng minh rằng C = 2 + 2 2 + 2 3 + . . . + 2 60 chia hết cho 3
Chứng minh rằng C = 2 + 2 2 + 2 3 + ... + 2 60 chia hết cho 3
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: C = 2 + 2 2 + 2 3 + 2 4 + ... + 2 59 + 2 60 = 2 1 + 2 + 2 3 1 + 2 + ... + 2 59 1 + 2 = 2.3 + 2 3 .3 + ... + 2 59 .3 = 2 + 2 3 + ... + 2 59 .3 ⇒ C ⋮ 3 |
Đúng 0
Bình luận (0)
Chứng minh rằng A = 2 + 2 2 + 2 3 + … + 2 60 chia hết cho 7.
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 7. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 + 2 2 + 2 3 + … + 2 60 = 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + … + 2 58 + 2 59 + 2 60 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2 + 2 4 + … + 2 58 .7 ⇒ A ⋮ 7 |
Đúng 0
Bình luận (0)