MM
Những câu hỏi liên quan

Mọi người làm câu 2,3 giúp e với ạ.E cảm ơn nhiều ạ
Câu 2:
a, Số hạt p, n, e lần lượt là:
- Trong nitrogen: 7,7,7
- Trong fluorine: 9, 10, 9
- Trong neon: 10, 10, 10
b, Hai hạt luôn có số lượng bằng nhau là: p và e
Đúng 1
Bình luận (0)

Mn giúp e vs ạ.Ai nhanh nhất đc mụt like,theo dõi và đc 1 coin ạ.E cảm ơn rất nhiều ạ.
Giúp e giải 2 câu này với ạ.E cảm ơn
a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(2t+t^2-1+1=0\)
\(\Rightarrow t\left(t+2\right)=0\Rightarrow\left[{}\begin{matrix}t=0\\t=-2< -\sqrt{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=0\)
\(\Rightarrow tanx=-1\)
\(\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
Đúng 1
Bình luận (0)
a, Đặt \(sinx+cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(pt\Leftrightarrow2t+t^2-1+1=0\)
\(\Leftrightarrow t^2+2t=0\)
\(\Leftrightarrow t\left(t+2\right)=0\)
\(\Leftrightarrow t=0\)
\(\Leftrightarrow sinx+cosx=0\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\)
Đúng 1
Bình luận (0)
b.
Đặt \(sinx-cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Phương trình trở thành:
\(2\sqrt{2}t-2\left(1-t^2\right)=1\)
\(\Leftrightarrow2t^2+2\sqrt{2}t-3=0\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{\sqrt{2}}{2}\\t=-\dfrac{3\sqrt{2}}{2}< -\sqrt{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{5}+k2\pi\end{matrix}\right.\)
\(\Rightarrow...\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tính tích các số lẻ trong dãy số nguyên dương . Mọi người giải giúp e ,mong mọi người ghi rõ chữ cho e hiểu với ạ.E rất rất cảm ơn
#include <bits/stdc++.h>
using namespace std;
long long n,i,s,x;
int main()
{
cin>>n;
s=1;
for (i=1; i<=n; i++)
{
cin>>x;
if (x%2!=0) s=s*x;
}
cout<<s;
return 0;
}
Đúng 0
Bình luận (0)
Giúp e chi tiết 3 câu này với ạ.E cảm ơn
1.
\(cos\left(\dfrac{2\pi}{3}+2x\right)+cos\left(\dfrac{\pi}{3}+x\right)+1=0\)
\(\Leftrightarrow2cos^2\left(\dfrac{\pi}{3}+x\right)+cos\left(\dfrac{\pi}{3}+x\right)=0\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{3}+x\right)\left[2cos\left(\dfrac{\pi}{3}+x\right)+1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{3}+x\right)=0\\cos\left(\dfrac{\pi}{3}+x\right)=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}+x=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{3}+x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Chào mn!!!hnay mình đăng câu hỏi này lên đây để nhờ những a/cj CTV hoặc CTVVIP giúp ạ.E nhờ là việc mỗi khi CTV hay là gv/ admin đăng bài là có mấy bạn vô đấy để hỏi toán hay tiếng việt,.... đã rất nhiều lần e gặp tình trạng này rùi ạ,MN muốn đăng câu hỏi thì ko nên đăng vào trả lời của GV/CTV/ CTVVIP ạ vì như thế sẽ trôi hết câu trả lời của các bạn, với lại các bạn muốn đăng câu hỏi thì tạo câu hỏi đàng hoàng mn sẽ trả lời giúp các bạn ạ.nhiều lần e nhắc nhưng các bạn ý ko nghe vẫn vi phạm, nên...
Đọc tiếp
Chào mn!!!
hnay mình đăng câu hỏi này lên đây để nhờ những a/cj CTV hoặc CTVVIP giúp ạ.
E nhờ là việc mỗi khi CTV hay là gv/ admin đăng bài là có mấy bạn vô đấy để hỏi toán hay tiếng việt,.... đã rất nhiều lần e gặp tình trạng này rùi ạ,
MN muốn đăng câu hỏi thì ko nên đăng vào trả lời của GV/CTV/ CTVVIP ạ vì như thế sẽ trôi hết câu trả lời của các bạn, với lại các bạn muốn đăng câu hỏi thì tạo câu hỏi đàng hoàng mn sẽ trả lời giúp các bạn ạ.
nhiều lần e nhắc nhưng các bạn ý ko nghe vẫn vi phạm, nên hôm nay e đăng lên đây muốn nhờ mấy a/ cj CTV/ CTVVIP giúp e ạ.
Em trân trọng cảm ơn!
Xem thêm câu trả lời
Mn ai biết giúp e vs ạ.E cảm ơn mn nhiều
Giúp e chi tiết bài 4 này với ạ.E cảm ơn nhiều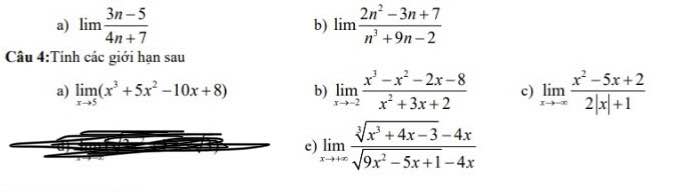
\(\lim\limits_{x\rightarrow5}\left(x^3+5x^2-10x+8\right)=5^3+5.5^2-10.5+8=...\)
\(\lim\limits_{x\rightarrow-2}\dfrac{x^3-x^2-2x-8}{x^2+3x+2}=\dfrac{-16}{0}=-\infty\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x^2-5x+2}{2\left|x\right|+1}=\lim\dfrac{\left|x\right|-5+\dfrac{2}{\left|x\right|}}{2+\dfrac{1}{\left|x\right|}}=\dfrac{+\infty}{2}=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{x^3+4x-3}-4x}{\sqrt{9x^2-5x+1}-4x}=\lim\limits_{x\rightarrow+\infty}\dfrac{x\left(\sqrt[3]{1+\dfrac{4}{x^2}-\dfrac{3}{x^3}}-4\right)}{x\left(\sqrt[]{9-\dfrac{5}{x}+\dfrac{1}{x^2}}-4\right)}=\dfrac{1-4}{3-4}=3\)
Đúng 1
Bình luận (0)
Lời giải:
a.
\(\lim\limits_{x\to 5}(x^3+5x^2-10x+8)=5^3+5.5^2-10.5+8=208\)
b.
\(L=\lim\limits_{x\to -2}\frac{x^3-x^2-2x-8}{x^2+3x+2}\lim\limits_{x\to -2}\frac{x^3-x^2-2x-8}{x+1}.\frac{1}{x+2}=16\lim\limits_{x\to -2}\frac{1}{x+2}\)\(\lim\limits_{x\to -2-}\frac{1}{x+2}=-\infty \Rightarrow L=-\infty ; \lim\limits_{x\to -2+}\frac{1}{x+2}=+\infty \Rightarrow L=+\infty \)
Đúng 1
Bình luận (0)
c.
\(\lim\limits_{x\to -\infty}\frac{x^2-5x+2}{2|x|+1}=\lim\limits_{x\to -\infty}\frac{|x|-\frac{5x}{|x|}+\frac{2}{|x|}}{2+\frac{1}{|x|}}\)
\(=\lim\limits_{x\to -\infty}\frac{|x|-\frac{5x}{-x}}{2}=\frac{1}{2}\lim\limits_{x\to -\infty}(|x|+5)=+\infty \)
Đúng 1
Bình luận (0)
Anh chị giúp e giải bài này với ạ.E cảm ơn nhiều lắm
a) \(\left(2m-1\right)sinx+1-m=0\Rightarrow sinx=\dfrac{m-1}{2m-1}\)
Pt có nghiệm: \(-1\le\dfrac{m-1}{2m-1}\le1\)
\(\Rightarrow1-2m\le m-1\le2m-1\Rightarrow m\ge\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
b) \(\left(m+1\right)sin3x-cos3x=m+2\)
Pt có nghiệm: \(\left(m+1\right)^2+\left(-1\right)^2\ge\left(m+2\right)^2\)
\(\Rightarrow m^2+2m+1+1\ge m^2+4m+4\)
\(\Rightarrow-2m\ge2\Rightarrow m\le-1\)
Đúng 0
Bình luận (0)
a, \(\left(2m-1\right)sinx+1-m=0\)
\(\Leftrightarrow sinx=\dfrac{m-1}{2m-1}\)
Phương trình có nghiệm khi:
\(-1\le\dfrac{m-1}{2m-1}\le1\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{2}{3}\\m\le0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời








