Cho x, y là hai số thỏa mãn : x + 2y = 3. Tìm giá trị nhỏ nhất của E = x2 + 2y2
help me
Cho hai số thực x,y thỏa mãn: 2 y 3 + 7 y + 2 x 1 - x = 3 1 - x + 3 ( 2 y 2 + 1 ) . Tìm giá trị lớn nhất của biểu thức P= x+2y
A. P = 8
B. P = 10
C. P= 4
D. P= 6
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
A. P = 3 + 2 2
B. P = 1 + 9 2
C. P = 9
D. Không tồn tại
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9 . 3 x 2 - 2 y = ( 4 + 9 x 2 - 2 y ) . 7 2 y - x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
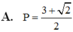
![]()
![]()
D. Không tồn tại
Cho hai số thực dương x,y thỏa mãn 2x + 2y = 4. Tìm giá trị lớn nhất Pmax của biểu thức
P = (2x2 + y)(2y2 + x) + 9xy.
A. Pmax = 27 2
B. Pmax = 18
C. Pmax = 27
D. Pmax = 12
Đáp án B.
Ta có 4 = 2 x + 2 y ≥ 2 2 x . 2 y = 2 2 x + y
⇔ 4 ≥ 2 x + y ⇔ x + y ≤ 2 .
Suy ra x y ≤ x + y 2 2 = 1
Khi đó
P = 2 x 3 + y 3 + 4 x 2 y 2 + 10 x y 2 x + y x + y 2 - 3 x y + 2 x y 2 + 10 x y
≤ 4 4 - 3 x y + 4 x 2 y 2 + 10 x y
= 16 + 2 x 2 y 2 + 2 x y x y - 1 ≤ 18
Vậy Pmax = 18 khi x = y = 1.
Cho x, y là số thực dương thỏa mãn log 2 x + log 2 y + 1 ≥ log 2 ( x 2 + 2 y ) Tìm giá trị nhỏ nhất của P = x + 2y
A. P = 9
B. P = 2 2 + 3
C. P = 2 + 3 2
D. P = 3 + 3
Cho hai số dương x,y thỏa mãn: 2x3-2x2+x2y+2xy2+y3-2y2=0
Tìm giá trị nhỏ nhất của biểu thức Q=\(\dfrac{3}{9x^2+6xy+y^2}=\dfrac{3}{3x^2+6xy+2y^2}\)
Chắc đề bài là \(Q=\dfrac{3}{9x^2+6xy+y^2}+\dfrac{3}{3x^2+6xy+2y^2}\)
Từ giả thiết ta có:
\(2x^3+2xy^2+xy^2+y^3=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x\left(x^2+y^2\right)+y\left(x^2+y^2\right)=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x+y=2\)
Do đó:
\(Q=3\left(\dfrac{1}{9x^2+6xy+y^2}+\dfrac{1}{3x^2+6xy+2y^2}\right)\)
\(Q\ge\dfrac{3.4}{12x^2+12xy+3y^2}=\dfrac{4}{\left(2x+y\right)^2}=1\)
\(Q_{min}=1\) khi \(\left\{{}\begin{matrix}2x+y=2\\9x^2+6xy+y^2=3x^2+6xy+2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{6}-2\\y=6-2\sqrt{6}\end{matrix}\right.\)
Cho hai số thực x, y thỏa mãn x ≥ 0 , y ≥ 1 , x + y = 3. Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 3 + 2 y 2 + 3 x 2 + 4 xy − 5 x .
A. P max = 15 v à P min = 13.
B. P max = 20 v à P min = 18
C. P max = 20 v à P min = 15.
D. P max = 18 v à P min = 15.
Cho hai số thực x,y thỏa mãn x ≥ 0 , y ≥ 1 , x + y = 3 . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 3 + 2 y 2 + 3 x 2 + 4 x y - 5 x .
A. P max = 15 và P min = 13 .
B. P max = 20 và P min = 18
C. P max = 20 và P min = 15
D. P max = 18 và P min = 18
Cho các số thực x, y dương và thỏa mãn log 2 x 2 + y 2 3 xy + x 2 + 2 log 2 x 2 + 2 y 2 + 1 ≤ log 2 8 xy .Tìm giá trị nhỏ nhất của biểu thức P = 2 x 2 - xy + 2 y 2 2 xy - y 2 .
Bài 4: Cho x, y là hai số thỏa mãn : x + 2y = 3. Tìm giá trị nhỏ nhất của E = x2 + 2y2
Bài 5 : Cho hai số x, y thỏa mãn : x2 + 3y2 + 2xy – 10x – 14y + 18 = 0. Tìm GTLN ; GTNN của biểu thức P = x + y
bài 4 : ta có : \(x+2y=3\Leftrightarrow x=3-2y\)
\(\Rightarrow E=x^2+2y^2=\left(3-2y\right)^2+2y^2=4y^2-12y+9+2y^2\)
\(=6y^2-12y+6+3=6\left(y-1\right)^2+3\ge3\)
\(\Rightarrow E_{max}=3\) khi \(x=y=1\)
bài 5 : ta có : \(x^2+3y^2+2xy-10x-14y+18=0\)
\(\Leftrightarrow2y^2-4y+2=-\left(x^2+2xy+y^2\right)+10\left(x+y\right)-16\)
\(\Leftrightarrow2\left(y-1\right)^2=-\left(x+y\right)^2+10\left(x+y\right)-16\ge0\)
\(\Leftrightarrow2\le x+y\le8\)
\(\Rightarrow P_{min}=2\) khi \(\left\{{}\begin{matrix}y=1\\x+y=2\end{matrix}\right.\Leftrightarrow x=y=1\)
\(\Rightarrow P_{max}=8\) khi \(\left\{{}\begin{matrix}y=1\\x+y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)
vậy ...........................................................................................................................