giải bất phương trình: |x+1|>|x-2|
Giải giùm đi ạ
H24
Những câu hỏi liên quan
chứng minh: 5x²+15x+20>0 với mọi x
giải phương trình: \2x\-3=\x+2\ ( phương trình chứa dấu giá trị tuyệt đối ) giải giùm tớ đi ạ
CM: 5x^2 +15x+20>0
Ta có: 5x^2 +15x +20
= 5( x^2 + 3x +4)
=5[(x^2 + 2.x.3/2 +9/4) -9/4 +4 ]
=5(x+3/2)^2 -7/4
Vì (x+3/2)^2 >0 với mọi x
=>5(x+3/2)^2 >0 với mọi x
=> 5(x+3/2)^2 - 7/4 >0 với mọi x
giải phương trình
(x+1)(x+2)(x+3)(x+4)+3 = 0 giải giùm mình zs ghi rõ nha tks nhìu ạ :*
Giải bất phương trình: |x + 1| - |x – 2|3 > 3
giúp em với ạ
giải phương trình và bất phương trình sau:
a, \(\dfrac{3}{x-1}=\dfrac{4}{x+1}\)
b,(x-1).(x-3)=0
c, 2(x-1)+x=0
mọi người giúp mình với ạ
a: =>3x+3=4x-4
=>-x=-7
hay x=7(nhận)
b: (x-1)(x-3)=0
=>x-1=0 hoặc x-3=0
=>x=1 hoặc x=3
c: 2(x-1)+x=0
=>2x-2+x=0
=>3x-2=0
hay x=2/3
Đúng 1
Bình luận (0)
a, ĐKXĐ : x ≠ 1 ; x ≠ -1
\(\Rightarrow3\left(x+1\right)=4\left(x-1\right)\)
\(\Leftrightarrow3x+3=4x-4\)
\(\Leftrightarrow-x=-7\)
\(\Leftrightarrow x=7\left(N\right)\)
b,
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
c,
\(\Leftrightarrow2x-2+x=0\)
\(\Leftrightarrow3x=2\)
\(\Leftrightarrow x=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
GIải bất phương trình : x+1/100+x+2/99<x+3/3+x+4/2
giúp mik vs mọi người ạ
x+1<x+2<x+3<x+4 ( với mọi x)
\(\dfrac{1}{100}\) < \(\dfrac{1}{99}\)<\(\dfrac{1}{3}\) <\(\dfrac{1}{2}\)
=>\(\dfrac{x+1}{100}\)+\(\dfrac{x+2}{99}\) <\(\dfrac{x+3}{3}\)+\(\dfrac{x+4}{2}\) là đúng
Đúng 0
Bình luận (0)
\(\frac{\left|x-1\right|+3}{\left|5-x\right|+x}< 4\)
Giải giùm mình bất phương trình này với
Giải bất phương trình ( Tìm x biết )
3(\(\frac{1}{3}\)-2) +x > x+\(\frac{1}{4}\)
Gảii giùm mik với. Thanks mọi người trc nha. Làm ơn nhanh lên giùm nha
1.Giải bất phương trình: 3* căn[1-(3/x)] + căn[3x-(27/x)] >= x
2. Tìm m để bất phương trình [(10-m)x^2-2(m+2)x+1]/[căn(x^2-2x+2] < 0 có nghiệm
Cảm ơn nhiều những ai giúp em ạ!
Giúp e với ạ Giải bất phương trình: (x ^ 2 - 3x + 2)/(9 - x ^ 2) >0
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(3-x\right)\left(3+x\right)}>0\)
Bảng xét dấu:
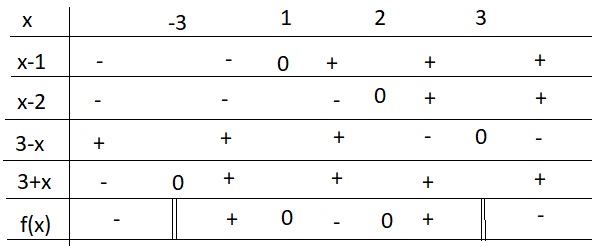
Từ bảng xét dấu ta có nghiệm của BPT là: \(x\in\left(-3;1\right)\cup\left(2;3\right)\)
Đúng 2
Bình luận (0)