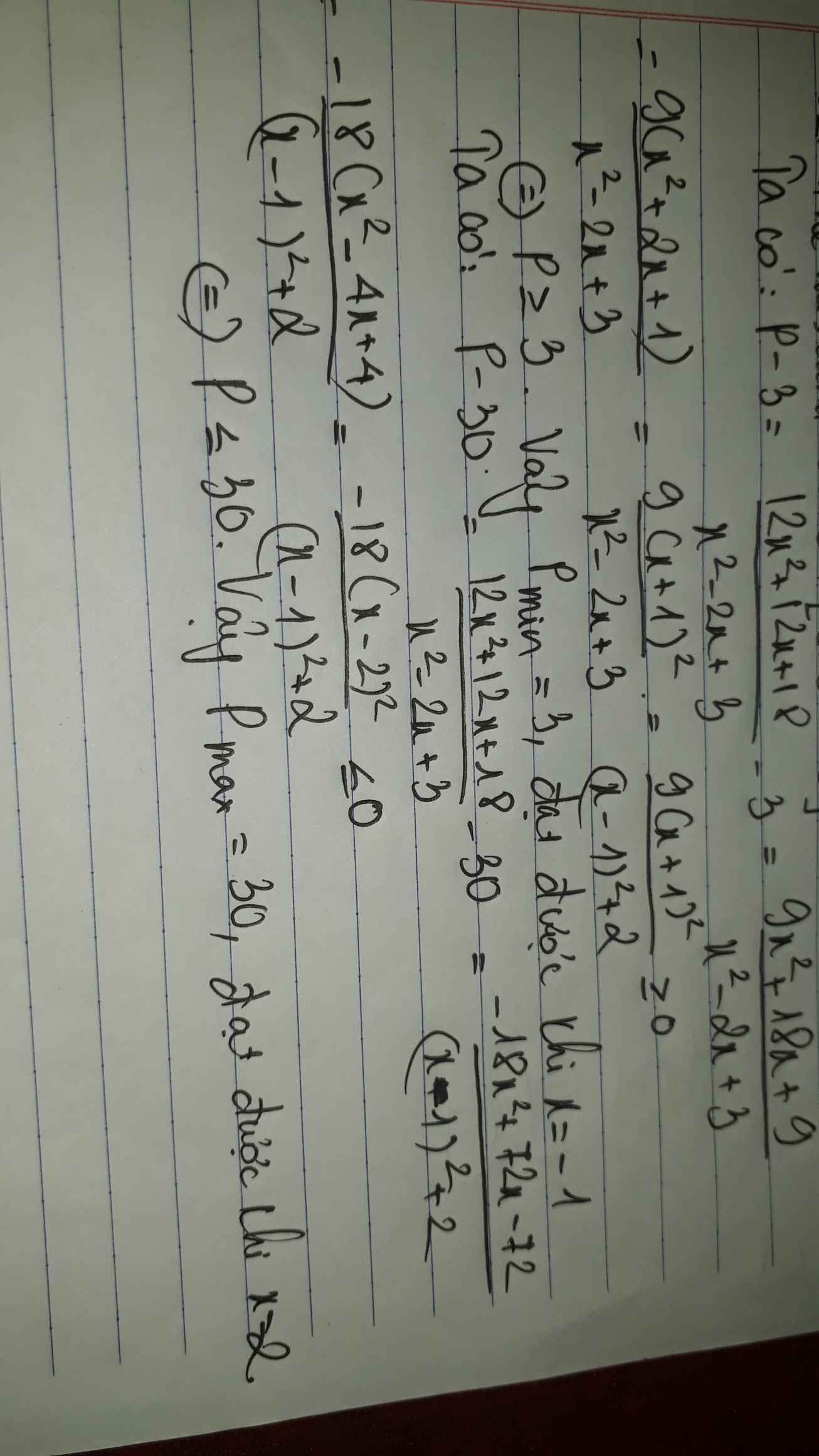giá trị lớn nhất của 12-3x^2+12x
TN
Những câu hỏi liên quan
1,TBC các giá trị x thoả mãn 4(x-1)^2=x^2
2,Giá trị nhỏ nhất x^2-2x-3
3,Giá trị nhỏ nhất của 3x^2-12x+1
4,Giá trị lớn nhất của 4x-x^2-12
Tìm giá trị nhỏ nhất lớn nhất của hàm số y=2X^3+3x^2-12x+1 trên [-1;5]?
\(y'=6x^2+6x-12=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(-1\right)=14\) ; \(y\left(1\right)=-6\) ; \(y\left(5\right)=266\)
\(\Rightarrow\min\limits_{\left[-1;5\right]}y=-6\) ; \(\max\limits_{\left[-1;5\right]}y=266\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của
A=x^2-10x+3
B=3x^2+7x-2
Tìm giá trị lớn nhất của
A= -9x^2+12x-5
B= -2x^2 -3x +7
Tìm GTNN
A = x2 - 10x + 3 = ( x2 - 10x + 25 ) - 22 = ( x - 5 )2 - 22 ≥ -22 ∀ x
Dấu "=" xảy ra khi x = 5
=> MinA = -22 <=> x = 5
B = 3x2 + 7x - 2 = 3( x2 + 7/3x + 49/36 ) - 73/12 = 3( x + 7/6 )2 - 73/12 ≥ -73/12 ∀ x
Dấu "=" xảy ra khi x = -7/6
=> MinB = -73/12 <=> x = -7/6
Tìm GTLN
A = -9x2 + 12x - 5 = -9( x2 - 4/3x + 4/9 ) - 1 = -9( x - 2/3 )2 - 1 ≤ -1 ∀ x
Dấu "=" xảy ra khi x = 2/3
=> MaxA = -1 <=> x = 2/3
B = -2x2 - 3x + 7 = -2( x2 + 3/2x + 9/16 ) + 65/8 = -2( x + 3/4 )2 + 65/8 ≤ 65/8 ∀ x
Dấu "=" xảy ra khi x = -3/4
=> MaxB = 65/8 <=> x = -3/4
giá trị x>0 để -3x^4+12x^2+1 đạt giá trị lớn nhất
\(-3x^4+12x^2+1=-3\left(x^4-4x^2+4\right)+12+1\)
\(=13-3\left(x^2-2\right)^2\le13\)
Đạt GTLN khi \(x=\sqrt{2}\)
Đúng 0
Bình luận (0)
tui nghĩ bài này phải là kiến thức lop9, thử xem sao, mong a2 xem giúp em
đặt t = x2có -3(t2 - 4t +4) +4 +1
GTLN = 5
Đúng 0
Bình luận (0)
ồ, em quên 4.3 = 12+1 = 13
em biết mà, chỉ có a2 mới giúp dc em thui,
cám ơn a2
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức a) C=-3x^2-12x+4 b) D=-x^2+5x c) M=2x-x^2
Lời giải:
a.
$C=16-3(x^2+4x+4)=16-3(x+2)^2$
Vì $(x+3)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow C\leq 16-3.0=16$
Vậy $C_{\max}=16$ khi $x=-2$
b.
$D=-x^2+5x=2,5^2-(x^2-5x+2,5^2)$
$=6,25-(x+2,5)^2\leq 6,25-0=6,25$
Vậy $D_{\max}=6,25$ khi $x=-2,5$
c.
$M=2x-x^2=1-(x^2-2x+1)=1-(x-1)^2\leq 1-0=1$
Vậy $M_{\max}=1$ khi $x=1$
Đúng 1
Bình luận (0)
a: Ta có: \(C=-3x^2-12x+4\)
\(=-3\left(x^2+4x-\dfrac{4}{3}\right)\)
\(=-3\left(x^2+4x+4-\dfrac{16}{3}\right)\)
\(=-3\left(x+2\right)^2+16\le16\forall x\)
Dấu '=' xảy ra khi x=-2
b: Ta có: \(D=-x^2+5x\)
\(=-\left(x^2-5x+\dfrac{25}{4}\right)+\dfrac{25}{4}\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
Đúng 0
Bình luận (0)
c: Ta có: \(M=-x^2+2x\)
\(=-\left(x^2-2x+1-1\right)\)
\(=-\left(x-1\right)^2+1\le1\forall x\)
Dấu '=' xảy ra khi x=1
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất:
A=12x - 3x2
Tìm giá trị nhỏ nhất của các biểu thức sau
E=(2x – 5)10 – 12 F=(x+5)8+|x+5|+ 22
Tìm giá trị lớn nhất của các biểu thức sau
G=17-|3x-2| K= 17-|3x-2|- (2-3x)2020
\(E=\left(2x-5\right)^{10}-12\ge-12\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{5}{2}\)
Vậy \(E_{min}=-12\Leftrightarrow x=\dfrac{5}{2}\)
\(F=\left(x+5\right)^8+\left|x+5\right|+22\ge22\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy \(F_{min}=22\Leftrightarrow x=-5\)
\(G=17-\left|3x-2\right|\)
Dấu "=" xảy ra \(x=\dfrac{2}{3}\)
Vậy \(G_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
\(K=17-\left|3x-2\right|-\left(2-3x\right)^{2020}\le17\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(K_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Cho A=(x+3)2−3x(6−x)+3
tìm giá trị nhỏ nhất của A
Cho B= 12x−1−(x+3)2
tìm giá trị lớn nhất của B
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
\(P=\dfrac{12x^2+12x+18}{x^2-2x+3}\)