Cho (d1) : y= –x +1
(d2) : y= –2x+4
a) Vẽ 2 đồ thị hs trên.
b) XĐ đường thẳng (d3) đi qua M(3;2) và \\ vs (d1)
c) XĐ (d4) đi qua M (3;2)và vuông góc vs (d2)
Cho hàm số y=-2x-2 có đồ thị là đường thẳng d1 A/ viết phương trình đường thẳng d2 biết rằng d2 đi qua điểm M (2;-2) và song song với đường thẳng d1 B/ vẽ d1 và d2 trên cùng một hệ trục tọa độ Oxy C/ cho hàm số y= x+m có đồ thị là đường thẳng d3, xác định tham số m để đường thẳng d1 cắt đường thẳng d3 trên trục Ox
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
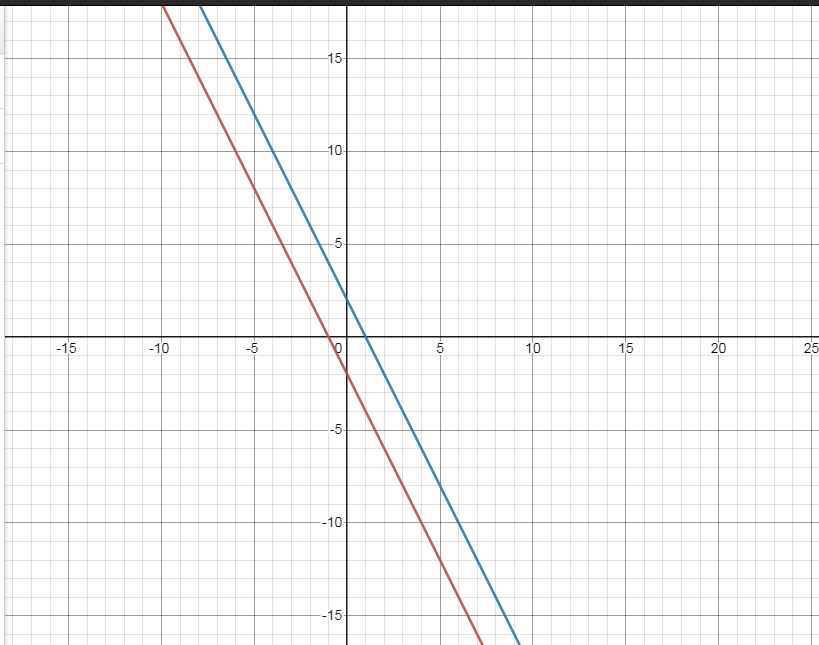
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)
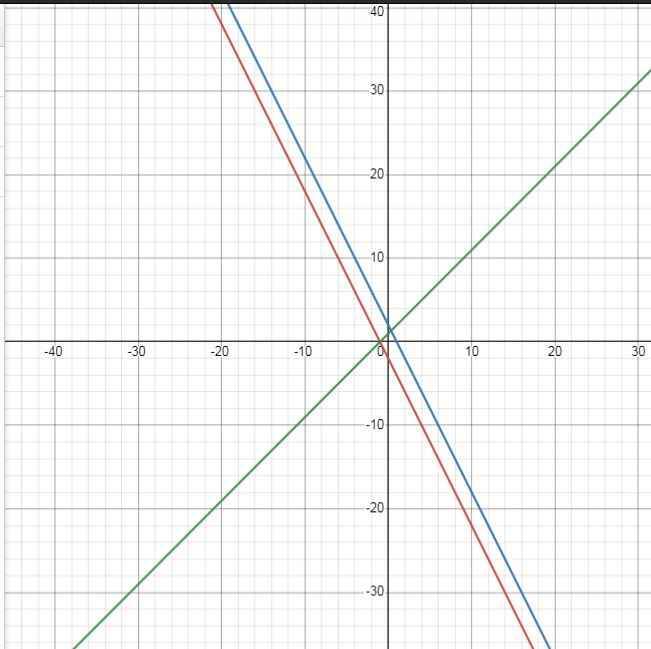
1/Cho hai đường thẳng (d1):y = x + 4 và (d2):y = - 2x - 2 a) Vẽ đồ thị (d1) và (d2) trên cùng một mặt phẳng tọa độ. b) Cho đường thẳng (d3): y = ax + b . Xác định a và b biết đường thẳng (d3) song song với đường thẳng (d1) và (d3) cắt (d2)tại điểm A có hoành độ là -3.
\(b,\left(d_3\right)\text{//}\left(d_1\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne4\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=x+b\)
PT hoành độ giao điểm \(\left(d_2\right);\left(d_3\right)\) là \(x+b=-2x-2\)
Mà 2 đt cắt tại hoành độ \(-3\) nên \(x=-3\)
\(\Leftrightarrow b-3=4\Leftrightarrow b=7\)
Vậy \(\left(d_3\right):y=x+7\)
cho hàm số y=-2x+3 có đồ thị là (d1)và hàm số y=x-1 có đồ thị là (d2) a. vẽ (d1)và (d2) trên cùng 1 mặt phẳng tọa độ b. tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính c. viết phương trình đường thẳng (d3) đi qua điểm A(-2;1) và song song với đường thẳng (d1)
a, Hàm số \(\left(d_1\right)y=-2x+3\)
Cho \(y=0=>x=\dfrac{3}{2}\) ta được điểm \(\left(\dfrac{3}{2};0\right)\)
Cho \(x=0=>y=3\) ta được điểm \(\left(0;3\right)\)
Vẽ đồ thị hàm số \(\left(d_1\right)\) đi qua hai điểm trên
hàm số \(\left(d_2\right)y=x-1\)
Cho \(y=0=>x=1\) ta được điểm \(\left(1;0\right)\)
Cho \(x=0=>y=-1\) ta được điểm \(\left(0;-1\right)\)
Vẽ đồ thị hàm số \(\left(d_2\right)\) đi qua hai điểm trên
# Bạn có thể tự vẽ nhé !!
b, Tọa độ giao điểm \(\left(d_1\right);\left(d_2\right)\) là nghiệm của pt
\(-2x+3=x-1\\ =>-3x=-4\\ =>x=\dfrac{4}{3}\)
Thay \(x=\dfrac{4}{3}\) vào \(\left(d_2\right)\)
\(\Rightarrow y=\dfrac{4}{3}-1=\dfrac{1}{3}\)
Vậy tọa độ giao điểm là : \(\left(\dfrac{4}{3};\dfrac{1}{3}\right)\)
c, Giả sử \(\left(d_3\right)y=ax+b\)
\(\left(d_3\right)\) đi qua \(A\left(-2;1\right)\) và song song với đường thẳng \(\left(d_1\right)y=-2x+3\)
\(\Rightarrow\left\{{}\begin{matrix}4a+b=1\\a=-2;b\ne3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}4.\left(-2\right)+b=1\\a=-2;b\ne3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=9\left(t/m\right)\\a=-2\end{matrix}\right.\)
Vậy \(d_3:y=-2x+9\)
#Rinz
cho hàm số y=-2x+3 có đồ thị là (d1)và hàm số y=x-1 có đồ thị là (d2)
a. vẽ (d1)và (d2) trên cùng 1 mặt phẳng tọa độ
b. tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính
c. viết phương trình đường thẳng (d3) đi qua điểm A(-2;1) và song song với đường thẳng (d1)
Cho hàm số \(y=2x+4\) có đồ thị là (d1) và hàm số \(y=-x+1\) có đồ thị là (d2)
a. Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ Oxy
b. Xác định các hệ số a, b của đường thẳng \(y=ax+b\) (d3). Biết (d3) song song với (d1) và (d3) cắt (d2) tại một điểm có hoành độ bằng 2
Cho hàm số y=2x+2(d1), y=-1/2x - 2(d2)
a) vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy
b)Tìm tọa độ giao điểm A của (d1) và (d2)
c)Viết phương trình đg thẳng(d3), bt (d3) đi qua A và song song với đường thẳng y=2-5x
b: Phương trình hoành độ giao điểm là:
\(2x+2=\dfrac{-1}{2}x-2\)
\(\Leftrightarrow x\cdot\dfrac{5}{2}=-4\)
hay x=-10
Thay x=-10 vào (d1), ta được:
\(y=-20+2=-18\)
\(c,\left(d_3\right)\) đi qua \(A\left(-10;-18\right)\) nên \(x=-10;y=-18\)
\(\left(d_3\right)\) có dạng \(y=ax+b\Leftrightarrow-18=-10a+b\left(1\right)\)
\(\left(d_3\right)//y=-5x+2\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b\ne2\end{matrix}\right.\)
Thay vào \(\left(1\right)\Leftrightarrow-18=-10\left(-5\right)+b\Leftrightarrow b=32\left(tm\right)\)
Vậy \(\left(d_3\right):y=-5x+32\)
Cho 3 đường thẳng: y=1/2x-1(d1); y=-2x-4(d2); y=1/2x-4(d3).
a) Vẽ đồ thị các hàm số trên cùng một trục tọa độ. Nhận xét vị trí của 3 đường thẳng trên.
b) Cho (d2) cắt (d1) và (d3) tại 2 điểm A và B; (d1) cắt trục Ox tại C. Tính diện tích tam giác ABC
trên cùng một hệ trục toạ độ , cho 3 đường thẳng (d1) (d2) (d3) lần lượt là đồ thị hàm số y=-2x+2,6=1/2x-3 và y=mx+n a)vẽ đồ thị (d1) (d2) trên cùng một hệ trục toạ độ b)tìm m,n để đường thẳng (d3) song song với (₫1) cắt (d2j tại điểm có tung ddoj bằng -1
Cho hàm số y = 2x có đồ thị (d1) và hàm số y = x - 1 có đồ thị (d2)
a.Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ
b.Xác định a,b của hàm số y = ax + b (d3).Biết (d3) song song (d2) và (d1) đi qua M(1;3)
\(b,\left(d_3\right)//\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne-1\end{matrix}\right.\left(1\right)\\ M\left(1;3\right)\in\left(d_3\right)\Leftrightarrow a+b=3\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Vậy \(\left(d_3\right):y=x+2\)
(d1): Cho x = 0 A(0,0) B(1,2) 1 2 C -1 D => y= 0 - A(0,0)
x = 1 => y = 2 - B(1,2)
(d2): Cho x= 0 => y= -1 -C(0,-1)
x = 1 => y = 0 - D(1,0)