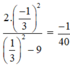Rút gọn rồi tính giá trị biểu thức tại x =2 ; y=3
M= \(2\left(x-y\right)^2-3\left(x+y\right)^2-\left(x-y\right)\left(x+y\right)+x\left(2x-5\right)\)
Giải giúp mình với mấy bạn ơi
1 a. Rút gọn biểu thức sau A = \(\left(x^{\text{2}}-2x+4\right):\left(x^3+8\right)-x^2\) rồi tính giá trị của A tại x = -2
b. Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
1 . Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
\(ĐK:x\ne0\)
Vậy tại x=0 thì k có gt nào của B thỏa mãn
rút gọn rồi tính giá trị của biểu thức A = x2-x -6 /x +2 tại x= -2
`A=(x^2-x-6)/x+2`
`=(x^2-x-6+2x)/x`
`=(x^2+x-6)/x`
`x=-2`
`=>A=(4+2-6)/(-2)`
`=0/(-2)`
`=0`
Ta có: \(A=\dfrac{x^2-x-6}{x+2}\)
\(=\dfrac{x^2-3x+2x-6}{x+2}\)
\(=\dfrac{x\left(x-3\right)+2\left(x-3\right)}{x+2}\)
\(=\dfrac{\left(x-3\right)\left(x+2\right)}{x+2}\)
=x-3
Vì x=-2 không thỏa mãn ĐKXĐ nên Khi x=-2 thì \(A\in\varnothing\)
Tính (rút gọn) đơn thức sao rồi tính giá trị biểu thức
(2/5x^3y).(-5xy) tại x = -1; y = 1/2
Đặt \(A=\left(\dfrac{2}{5}x^3y\right)\cdot\left(-5xy\right)\)
\(=\left(\dfrac{2}{5}\cdot\left(-5\right)\right)\cdot x^3\cdot x\cdot y\cdot y\)
\(=-2x^4y^2\)
Thay x=-1 và y=1/2 vào A, ta được:
\(A=-2\cdot\left(-1\right)^4\cdot\left(\dfrac{1}{2}\right)^2=-2\cdot\dfrac{1}{4}=-\dfrac{1}{2}\)
Tính (rút gọn) đơn thức sao rồi tính giá trị biểu thức
(2/5x^3y).(-5xy) tại x = -1; y = 1/2
Rút gọn rồi tính giá trị của biểu thức sau tại x = 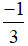 .
.
Tham khảo:
* Rút gọn biểu thức:
+ Ngoặc thứ nhất:
+ Ngoặc thứ hai:
Do đó:
* Tại 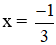
Rút gọn rồi tính giá trị biểu thức B = (x + 2y)(x^2 − 2xy + 4y^2) tại x = −8; y = −2
\(B=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ =\left(x+2y\right)\left(x^2-x.2y+\left(2y\right)^2\right)\\ =x^3+\left(2y\right)^3\\ =\left(-8\right)^3+\left(2.-2\right)^3\\ =\left(-8\right)^3+\left(-4\right)^3\\ =-512+\left(-64\right)\\ =-512-64=-576\)
\(B=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
\(=x\left(x^2-2xy+4y^2\right)+2y\left(x^2-2xy+4y^2\right)\)
\(=x^3-2x^2y+4xy^2+2x^2y-4xy^2+8y^3\)
\(=x^3+8y^3+\left(-2x^2y+2x^2y\right)+\left(4xy^2-4xy^2\right)\)
\(=x^3+8y^3\)
Thay \(x=-8;y=-2\) vào \(B\), ta được:
\(B=\left(-8\right)^3+8\cdot\left(-2\right)^3\)
\(=-512-64\)
\(=-576\)
Vậy \(B=-576\) tại \(x=-8;y=-2.\)
#\(Toru\)
Bài 2: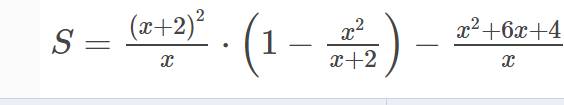
a) tìm điều kiện xác định của biểu thức S
b) Rút gọn rồi tính giá trị của biểu thức S tại x=0;1
c) tìm giá trị lớn nhất của biểu thức S
a) ĐKXĐ: \(x\ne0;x\ne-2\)
b) \(S=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{x+2-x^2}{x+2}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)\left(x+2-x^2\right)}{x}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{x^2+2x-x^3+2x+4-2x^2-x^2-6x-4}{x}\)
\(=\dfrac{-x^3-2x^2-2x}{x}\)
\(=\dfrac{x\left(-x^2-2x-2\right)}{x}\)
\(=-x^2-2x-2\)
Với \(x=0\Rightarrow\) loại
Với \(x=1\), thay vào \(S\) ta được
\(S=-1^2-2\cdot1-2=-5\)
c) Có: \(S=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)\)
\(=-\left(x^2+2x+1\right)-1\)
\(=-\left(x+1\right)^2-1\)
Ta thấy: \(\left(x+1\right)^2\ge0\forall x\ne0;x\ne-2\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\ne0;x\ne-2\)
\(\Rightarrow S=-\left(x+1\right)^2-1\le-1\forall x\ne0;x\ne-2\)
Dấu \("="\) xảy ra khi: \(x+1=0\Leftrightarrow x=-1\left(tmdk\right)\)
\(\text{#}\mathit{Toru}\)
Rút gọn rồi tính giá trị của biểu thức x 2 5 x + 25 + 2 x − 5 x + 50 + 5 x x x + 5 tại x = -2
Rút gọn rồi tính giá trị của biểu thức sau tại x = -1/3.
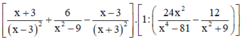
* Rút gọn biểu thức:
+ Ngoặc thứ nhất:
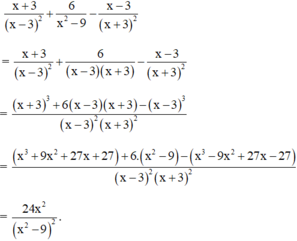
+ Ngoặc thứ hai:
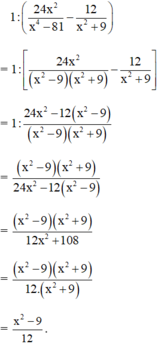
Do đó:
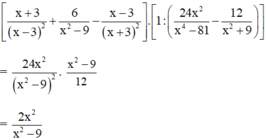
* Tại 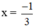 , giá trị biểu thức bằng:
, giá trị biểu thức bằng: