Em còn mỗi câu d thôi mn giúp e với
MN ơi giúp mình với còn câu d) chưa làm đc thôi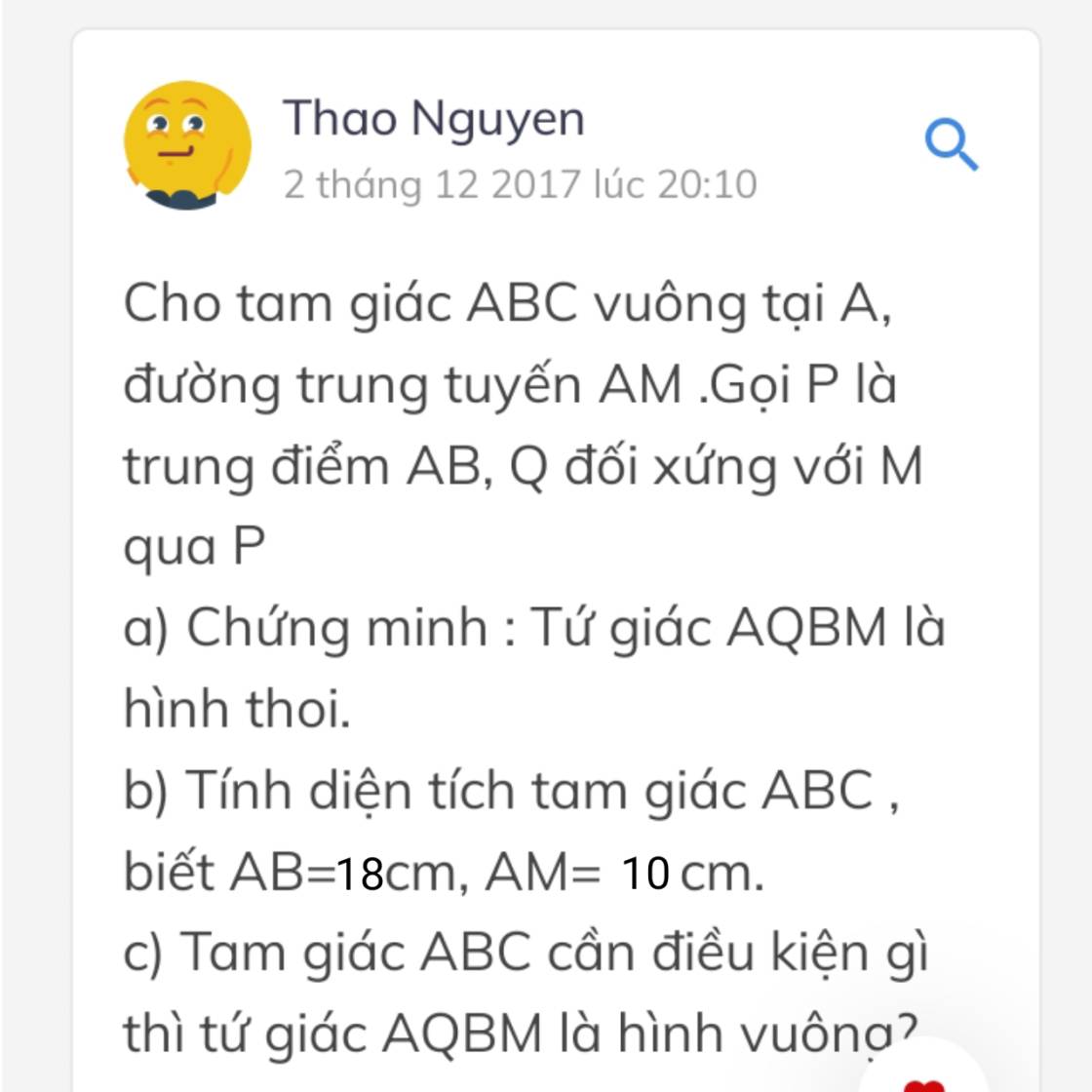
Mn giúp em làm bài hình này câu c d thôi ạ đc không ạ?:)
E xin cảm ơn

Giúp với còn 4 câu thôi giúp nhà mn

xin lỗi vì đã lm phiền mn ạ, giải hộ em với, em lm hết a với b rồi nên a chị nào giúp em câu c và d với ạ, đc sử dụng dữ kiện của câu trên nhé. GT ( đề bài ) ở bên phải hình vẽ ạ. HTC là hình thag cân ạ, còn cái (n) trong GT là cắt >< Mong mn giúp e ạ
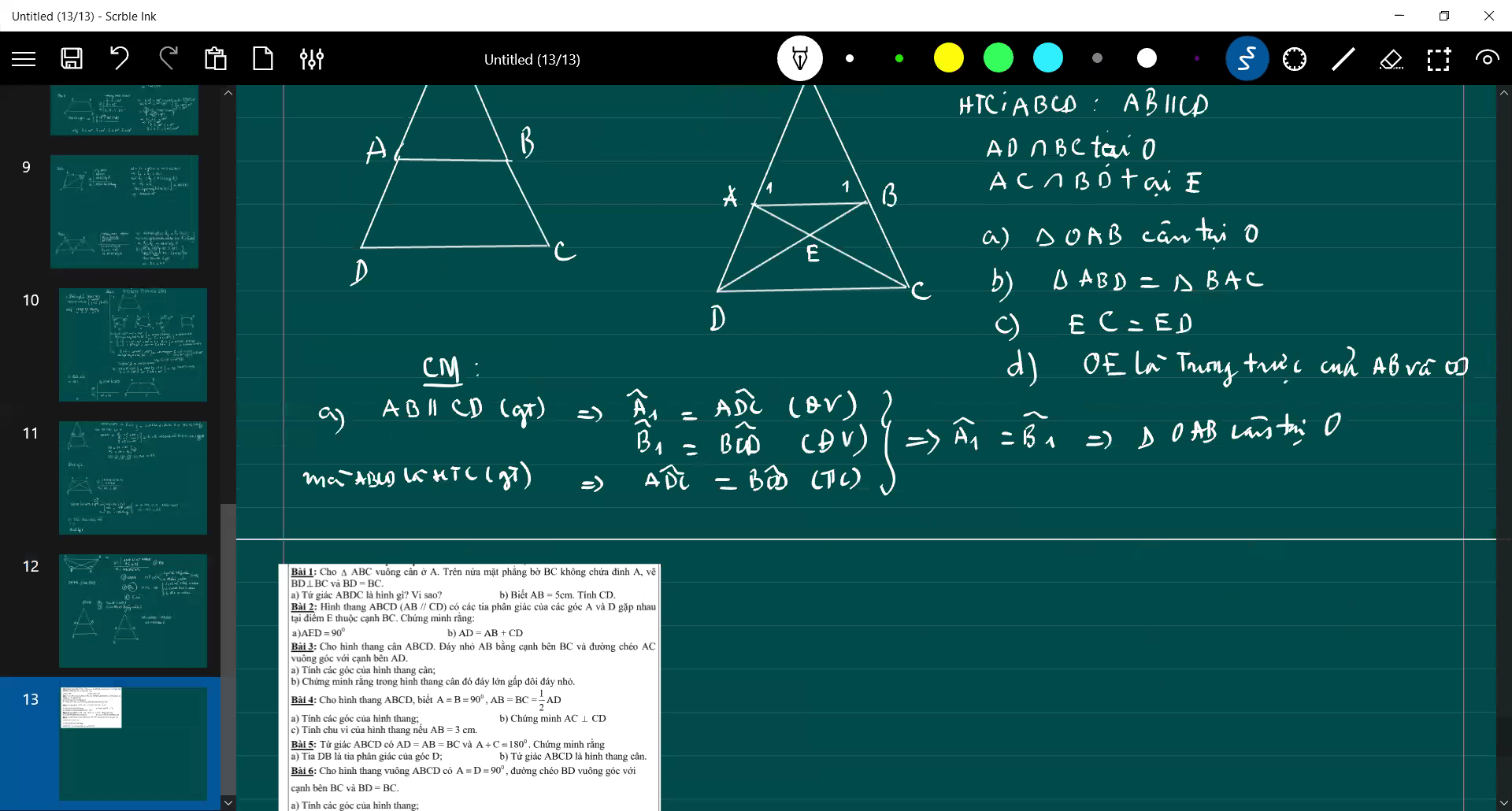
có j thắc mắc thì mn cứ hỏi ạ, em cần trc sáng mai nhé!? ><
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
Mn giúp e làm mấy câu còn lại với ạ e đang cần gấp. Em cảm ơn trc ạ

7. How often does he go to the library?
8. ....is the shortest student in his class.
9......is her address?
10... is shorter than Ba.
7 how often does he go to the library
8 nga is the shortest student in the class
9 what is her adress
10 hoa is shorter than ba
A/ Vẽ 1 đường thẳng cắt 2 đường thẳng. Trong các góc tạo thành có 1 cặp góc so le trong = nhau. Đặt tên cho các góc đó.
b/ vì sao cặp góc so le trong còn lại cũng = nhau?
c/ vì sao mỗi cặp góc đồng vị = nhau?
d/ vì sao mỗi cặp góc trong cùng phía bù nhau?
e/ vì sao mỗi cặp góc ngoài cùng phía bù nhau?
Em làm đc câu a,b rồi ạ. Mong mn giúp em câu c,d,e với ạ! Em cám ơn mn❤️
Mình làm xong hết rồi còn mỗi câu D thôi giúp mình với !,!,
bn có thể viết rõ ra ko . mờ quá ,chữ xấu nữa
Giúp em với mn, câu c thôi ạ. Giải chi tiết (ko tắt) hộ em với ạ

a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)