Tìm x
0,(12) : 1,(6) = x : 0,(3)
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
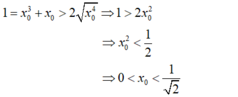
Tìm số tự nhiên (x0;y0) thỏa mãn:(2x+1)(y-5)=12
sao cho x0;y0 lớn nhất
minh ko biet xin loi ban nha!
minh ko biet xin loi ban nha!
minh ko biet xin loi ban nha!
minh ko biet xin loi ban nha!
mk k biet xn loi ban nha!
mk k biet xn loi ban nha!
mk k biet xn loi ban nha!
mk k biet xn loi ban nha!
Số?
a)12 x 4= ? x 12 (17x5)x2=17x(5x?)
106 x 3 =3 x ? 86x2x5=86 x(2x?)
b)7x ? =7 519 x ? =0 ? x0=0
432 x? =432 1x ? = 0 ?x1 =3456
a)
12 × 4 = 4 × 12
106 × 3 = 3 × 106
(17 × 5) × 2 = 17 × (5 × 2)
86 × 2 × 5 = 86 × (2 × 5)
b)
7 × 1 = 7
432 × 1 = 432
519 × 0 = 0
1 × 0 = 0
2 × 0 = 0
3 456 × 1 = 3 456
Lời giải:
Lấy $x_1\neq x_2\in\mathbb{R}$. Để hàm số đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{(3m-6)(x_1^2-x_2)^2}{x_1-x_2}=(3m-6)(x_1+x_2)>0$
Khi $x>0$ thì $x_1+x_2>0$. Để $y$ đồng biến khi $x>0$ thì $3m-6>0\Leftrightarrow m>2$
Khi $x<0$ thì $x_1+x_2< 0$. Để $y$ đồng biến khi $x< 0$ thì $3m-6< 0\Leftrightarrow m< 2$
Tìm a để các hàm số sau liên tục tại x0
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{1-x}+\sqrt{1+x}}{x}khix< 0\\a+\dfrac{4-x}{x+2}khi\ge0\end{matrix}\right.\)tại x0 = 0
Lời giải:
Để hàm số trên liên tục tại $x_0=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}(a+\frac{4-x}{x+2})=\lim\limits_{x\to 0-}(\frac{\sqrt{1-x}+\sqrt{1+x}}{x})=a+2\)
\(\Leftrightarrow a+2=\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}\)
Mà \(\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}=-\infty \) nên không tồn tại $a$ để hàm số liên tục tại $x_0=0$
Tìm các giá trị của x thỏa mãn
a.(x-3).(x-5)>0
b.(1/2+x0.(1/5+x)<0
c.(x+100).(x-100)<0
d.(2x-1).(x-3)>0
c.(x+3).(x-4)>0
Tìm các giá trị của x thỏa mãn
a.(x-3).(x-5)>0
b.(1/2+x0.(1/5+x)<0
c.(x+100).(x-100)<0
d.(2x-1).(x-3)>0
c.(x+3).(x-4)>0
Tìm x;
a) (-x+5)(3-x)=0
b) x(2+x)(7-x0)=0
a) TH1 -x+5=0 => x=5
TH2 3-x=0=>x=3
vậy x=5 hoặc x=3
b) TH1 x=0
TH2 2+x=0=> x=-2
TH3 7-x=0=> x=7
vậy x=0 hoặc x=-2 hay x=7
Tìm x biết: b/(x-2)^3+6(x+1)^2-x^3+12=0
\(\left(x-2\right)^3+6\left(x+1\right)^2-x^3+12=0\)
\(\Leftrightarrow x^3-6x^2+12x-8+6x^2+12x+6-x^3+12=0\)
\(\Leftrightarrow24x+10=0\)
\(\Leftrightarrow x=-\dfrac{5}{12}\)