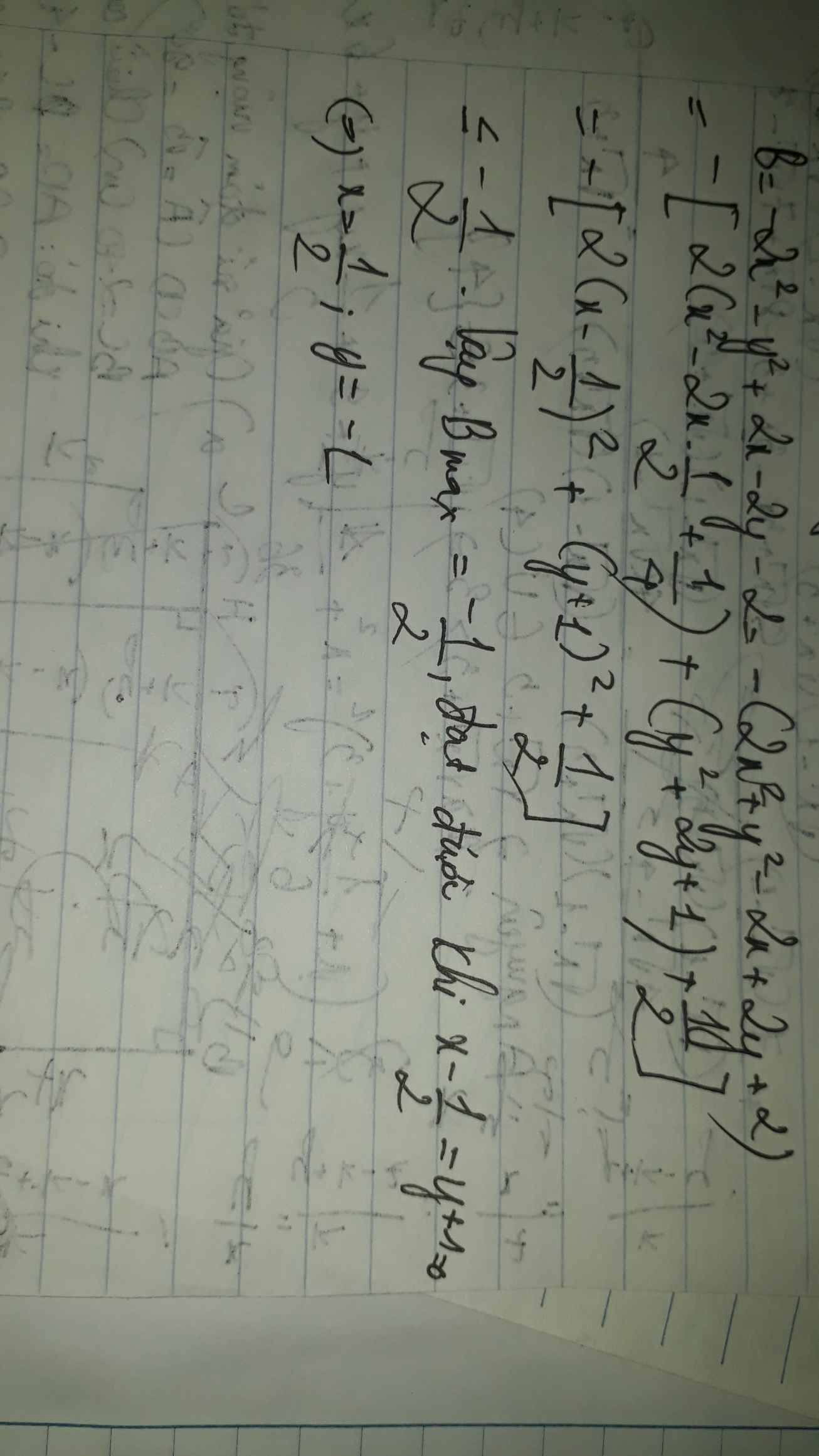a) x³+4x-5 = x³-x²+x²+4x-5=(x³-x²)+(x²-x)+(5x-5)=x²(x-1)+x(x-1)+5(x-1)=(x²+x+5)(x-1)

b) x³-3x²+4=x³-2x²-x²+4=(x³-2x²)-(x²-4)=x²(x-2)-(x-2)(x+2)=(x²-x+2)(x-2)

c) x³+2x²+3x+2=x³+x²+x²+x+2x+2=(x³+x²)+(x²+x)+(2x+2)=x²(x+1)+x(x+1)+2(x+1)=(x²+x+2)(x+1)

d) bạn xem lại đề đúng ko

e) (x²+3x)²-2(x²+3x)-8=x⁴+6x³+9x²-2x²-6x-8=x⁴+6x³+7x²-6x-8=x⁴-x³+7x³-7x²+14x²-14x+8x-8=(x⁴-x³)+(7x³-7x²)+(14x²-14x)+(8x-8)=x³(x-1)+7x²(x-1)+14x(x-1)+8(x-1)=(x³+7x²+14x+8)(x-1)=(x³+x²+6x²+6x+8x+8)(x-1)=\(\left[\left(x^3+x^2\right)+\left(6x^2+6x\right)+\left(8x+8\right)\right]\left(x-1\right)\)\(=\left[x^2\left(x+1\right)+6x\left(x+1\right)+8\left(x+1\right)\right]\left(x-1\right)\)\(=\left(x^2+6x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left(x^2+2x+4x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left[\left(x^2+2x\right)+\left(4x+8\right)\right]\left(x+1\right)\left(x-1\right)\)\(=\left[x\left(x+2\right)+4\left(x+2\right)\right]\left(x+1\right)\left(x-1\right)\)=\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x+4\right)\)

f) (x²+4x+10)²-7(x²+4x+11)+7=(x²+4x+10)²-\(\left[7\left(x^2+4x+11\right)-7\right]\)\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)\)\(=\left(x^2+4x+10\right)\left(x^2+4x+3\right)\)

a) Ta có: \(x^3+4x-5\)

\(=x^3-x+5x-5\)

\(=x\left(x-1\right)\left(x+1\right)+5\left(x-1\right)\)

\(=\left(x-1\right)\left(x^2+x+5\right)\)

b) Ta có: \(x^3-3x^2+4\)

\(=x^3+x^2-4x^2+4\)

\(=x^2\left(x+1\right)-4\left(x-1\right)\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2-4x+4\right)\)

\(=\left(x+1\right)\cdot\left(x-2\right)^2\)

c) Ta có: \(x^3+2x^2+3x+2\)

\(=x^3+x^2+x^2+x+2x+2\)

\(=x^2\left(x+1\right)+x\left(x+1\right)+2\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2+x+2\right)\)

d) Ta có: \(x^2+2xy+y^2+2x+2y-3\)

\(=\left(x+y\right)^2+2\left(x+y\right)-3\)

\(=\left(x+y\right)^2+3\left(x+y\right)-\left(x+y\right)-3\)

\(=\left(x+y\right)\left(x+y+3\right)-\left(x+y+3\right)\)

\(=\left(x+y+3\right)\left(x+y-1\right)\)

e) Ta có: \(\left(x^2+3x\right)^2-2\left(x^2+3x\right)-8\)

\(=\left(x^2+3x\right)^2-4\left(x^2+3x\right)+2\left(x^2+3x\right)-8\)

\(=\left(x^2+3x\right)\left(x^2+3x-4\right)+2\left(x^2+3x-4\right)\)

\(=\left(x^2+3x-4\right)\left(x^2+3x+2\right)\)

\(=\left(x+4\right)\left(x-1\right)\left(x+1\right)\left(x+2\right)\)

f) Ta có: \(\left(x^2+4x+10\right)^2-7\left(x^2+4x+11\right)+7\)

\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)-7+7\)

\(=\left(x^2+4x+10\right)\left(x^2+4x+10-7\right)\)

\(=\left(x^2+4x+3\right)\left(x^2+4x+10\right)\)

\(=\left(x+1\right)\left(x+3\right)\left(x^2+4x+10\right)\)

+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.

+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :

a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0

⇒ phương trình trên là phương trình đường tròn.

+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :

a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0

⇒ phương trình trên không là phương trình đường tròn.

+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :

a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0

⇒ phương trình trên không là phương trình đường tròn.

\(a.\left(x^2+4x+4\right)+\left(x^2-6x+9\right)=2x^2+14x\)

\(x^2+4x+4+x^2-6x+9-2x^2-14x=0\)

\(-18x+13=0\)

\(x=\dfrac{13}{18}\)

Vậy \(S=\left\{\dfrac{13}{18}\right\}\)

\(b.\left(x-1\right)^3-125=0\)

\(\left(x-1\right)^3=125\)

\(x-1=5\)

\(x=6\)

Vậy \(S=\left\{6\right\}\)

\(c.\left(x-1\right)^2+\left(y +2\right)^2=0\)

\(Do\left(x-1\right)^2\ge0\forall x;\left(y+2\right)^2\ge0\forall y\)

\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\forall x,y\)

Mà \(\left(x-1\right)^2+\left(y+2\right)^2=0\)

\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

Vậy \(S=\left\{1;-2\right\}\)

\(d.x^2-4x+4+x^2-2xy+y^2=0\)

\(\left(x-2\right)^2+\left(x-y\right)^2=0\)

\(\Rightarrow\left[{}\begin{matrix}\left(x-2\right)^2=0\\\left(x-y\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

Vậy \(S=\left\{2;2\right\}\)

ĐK:  y − 2 x + 1 ≥ 0 , 4 x + y + 5 ≥ 0 , x + 2 y − 2 ≥ 0 , x ≤ 1

T H 1 :   y − 2 x + 1 = 0 3 − 3 x = 0 ⇔ x = 1 y = 1 ⇒ 0 = 0 − 1 = 10 − 1 ( k o   t / m ) T H 2 :   x ≠ 1 , y ≠ 1  

Đưa pt thứ nhất về dạng tích ta được

( x + y − 2 ) ( 2 x − y − 1 ) = x + y − 2 y − 2 x + 1 + 3 − 3 x ( x + y − 2 ) 1 y − 2 x + 1 + 3 − 3 x + y − 2 x + 1 = 0 ⇒ 1 y − 2 x + 1 + 3 − 3 x + y − 2 x + 1 > 0 ⇒ x + y − 2 = 0

Thay y= 2-x vào pt thứ 2 ta được  x 2 + x − 3 = 3 x + 7 − 2 − x

⇔ x 2 + x − 2 = 3 x + 7 − 1 + 2 − 2 − x ⇔ ( x + 2 ) ( x − 1 ) = 3 x + 6 3 x + 7 + 1 + 2 + x 2 + 2 − x ⇔ ( x + 2 ) 3 3 x + 7 + 1 + 1 2 + 2 − x + 1 − x = 0

Do  x ≤ 1 ⇒ 3 3 x + 7 + 1 + 1 2 + 2 − x + 1 − x > 0

Vậy  x + 2 = 0 ⇔ x = − 2 ⇒ y = 4 (t/m)

a: \(2x^2+2x+1=0\)

\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)

Vì Δ<0 nên phương trình vô nghiệm

a) \(2x^2+2x+1=0\)

\(\Rightarrow2x^2+2x=-1\)

\(\Rightarrow2x\left(x+1\right)=-1\)

⇒ Pt vô nghiệm

b) \(x^2+y^2+2xy+2x+2y+1=0\)

\(\Rightarrow\left(x^2+y^2+2xy\right)+\left(2x+2y+1\right)=0\)

\(\Rightarrow\left(x+y\right)^2+2\left(x+y+1\right)=0\)

\(\Rightarrow\left\{{}\begin{matrix}\left(x+y\right)^2=0\\2\left(x+y+1\right)=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x+y=0\\x+y+1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x+y=0\\x+y=-1\end{matrix}\right.\)

⇒ Pt vô nghiệm

\(2x^2\)+\(y^2\)-2xy+2x+2y+5=0

(\(x^2-2xy+y^2\))+2(x+y)+4+(\(x^2+1\))=0

(x-y)² +2(x+y)+\(2^2\)+(\(x^2+1\))=0

(x-y+2)² +(\(x^2+1\))=0

Với mọi x;y Thuộc R thì (x-y+2)² >=0;\(x^2+1\)>0

suy ra (x-y+2)² +\(x^2+1\)>0

Do đó không tìm được giá trị nào của x;y để 2x² +\(y^2\)-2xy+2x+2y+5=0

Vậy không tìm đc giá trị nào của x;y thỏa mãn 2x² +\(y^2\) -2xy+2x+2y+5=0

chúc bạn học tốt ạ

1) Ta có: \(x^2-4x+4=0\)

\(\Leftrightarrow\left(x-2\right)^2=0\)

\(\Leftrightarrow x-2=0\)

hay x=2

Vậy: S={2}

a. 

$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$

b.

$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$

c.

$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$

d.

$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$

$=(x+1)(x^2-4x+1)$

e.

$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$

$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$

f.

$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$

$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$

g.

$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$

$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$

$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$

$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$

h.

$x^6+2x^5+x^4-2x^3-2x^2+1$

$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$

$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

Xem lại đề.

Ta có: \(B=-2x^2-y^2+2x-2y-2\)

\(=-\left(2x^2+y^2-2x+2y+2\right)\)

\(=-\left(2x^2-2x+\dfrac{1}{2}+y^2+2y+1+\dfrac{1}{2}\right)\)

\(=-2\left(x-\dfrac{1}{2}\right)^2-\left(y+1\right)^2-\dfrac{1}{2}\le\dfrac{1}{2}\forall x,y\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\) và y=-1