Tìm x \(\in\) Z để A = \(\dfrac{7}{\sqrt{x+3}}\)có giá trị là một số nguyên.
VN
Những câu hỏi liên quan
Bài 13 : Cho A =\(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\). Tìm x thuộc Z để A có giá trị là một số nguyên
Để A có giá trị là một số nguyên thì:
\(\left(\sqrt{x}+1\right)⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)+4⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow4⋮\left(\sqrt{x}-3\right)\)
Vì \(x\in Z\) nên \(\left(\sqrt{x}-3\right)\inƯ\left(4\right)=\left\{\pm1,\pm2,\pm4\right\}\)
Ta có bảng sau:
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| \(\sqrt{x}\) | 4 | 2 | 5 | 1 | 7 | -1 |
| x | 16 | 4 | 25 | 1 | 49 | (loại) |
Vậy ....
Đúng 0
Bình luận (0)
Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)+4}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}-3}=\dfrac{4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
Để A có giá trị là một số nguyên khi:
\(4⋮\sqrt{x}-3\) hay \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Do đó:
\(\sqrt{x}-3=-1\Rightarrow\sqrt{x}=-1+3=2\Rightarrow x=4\)
\(\sqrt{x}-3=1\Rightarrow\sqrt{x}=1+3=4\Rightarrow x=16\)
\(\sqrt{x}-3=-2\Rightarrow\sqrt{x}=-2+3=1\Rightarrow x=1\)
\(\sqrt{x}-3=2\Rightarrow\sqrt{x}=2+3=5\Rightarrow x=25\)
\(\sqrt{x}-3=-4\Rightarrow\sqrt{x}=-4+3=-1\) ( loại )
\(\sqrt{x}-3=4\Rightarrow\sqrt{x}=4+3=7\Rightarrow x=49\)
Vậy để A là một số nguyên khi \(x\in\left\{4;16;1;25;49\right\}\)
Đúng 0
Bình luận (0)
Cho \(B=\dfrac{2}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
Tìm \(x\in Z\) để B có giá trị nguyên
\(B=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}-2+2\sqrt{x}+x-3\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
Để B nguyên thì \(\sqrt{x}-3\in\left\{1;-1;5\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;8\right\}\)
hay \(x\in\left\{16;4;64\right\}\)
Đúng 0
Bình luận (0)
cho\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)tìm số nguyên x để A có giá trị là một số nguyên
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
Để A nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3+4⋮\sqrt{x}-3\)
mà \(\sqrt{x}-3⋮\sqrt{x}-3\)
nên \(4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\inƯ\left(4\right)\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
mà \(\sqrt{x}\ge0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}\in\left\{1;2;4;5;7\right\}\)
hay \(x\in\left\{1;4;16;25;49\right\}\)(nhận)
Vậy: Để A nguyên thì \(x\in\left\{1;4;16;25;49\right\}\)
Đúng 1
Bình luận (0)
Cho 2 biểu thức A= \(\dfrac{7}{\sqrt{x}+8}\) và B=\(\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-24}{x-9}\)
a) Chứng minh B= \(\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
b) Tìm GTLN của B
c) Tìm số nguyên x để biểu thức P = A.B có giá trị là số nguyên.
a, cho A dfrac{sqrt{x+1}}{sqrt{x-3}}. tìm x để A có giá trị nguyên ( x ϵ Z)b, Thực hiện phép tính: {[(2sqrt{2})^2 : 2,4] x [5,25 : (sqrt{7})^2]} : {[2dfrac{1}{7} : dfrac{left(sqrt{5}right)^2}{7}] : [2^2 : dfrac{left(2sqrt{2}right)^2}{sqrt{81}}]}
Đọc tiếp
a, cho A = \(\dfrac{\sqrt{x+1}}{\sqrt{x-3}}\). tìm x để A có giá trị nguyên ( x ϵ Z)
b, Thực hiện phép tính: {[(2\(\sqrt{2}\))\(^2\) : 2,4] x [5,25 : (\(\sqrt{7}\))\(^2\)]} : {[2\(\dfrac{1}{7}\) : \(\dfrac{\left(\sqrt{5}\right)^2}{7}\)] : [2\(^2\) : \(\dfrac{\left(2\sqrt{2}\right)^2}{\sqrt{81}}\)]}
a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
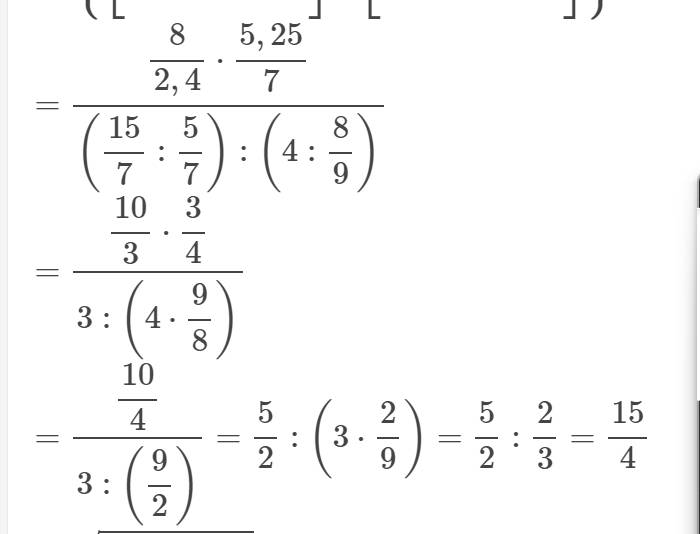
Đúng 0
Bình luận (0)
Tìm x để
a) A=\(\dfrac{x^2+3x-1}{x+2}\) có giá trị là số nguyên (x ϵ Z)
b) B=\(\dfrac{x^2+x+3}{x+1}\) có giá trị là số nguyên (x ϵ Z)
a: ĐểA nguyên thì x^2+2x+x+2-3 chia hết cho x+2
=>-3 chia hết cho x+2
=>x+2 thuộc {1;-1;3;-3}
=>x thuộc {-1;-3;1;-5}
b: B nguyên khi x^2+x+3 chia hết cho x+1
=>3 chia hết cho x+1
=>x+1 thuộc {1;-1;3;-3}
=>x thuộc {0;-2;2;-4}
Đúng 2
Bình luận (0)
Tìm \(x\in Z\) để biểu thức dưới đây nhận giá trị nguyên:
\(\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
tìm các số nguyên x để biểu thức sau có giá trị nguyên
a, A = \(\dfrac{7}{\sqrt{x}}\)
b, B = \(\dfrac{3}{\sqrt{x-1}}\)
c, C = \(\dfrac{2}{\sqrt{x-3}}\)
a: ĐKXĐ: x>0
Để A là số nguyên thì \(7⋮\sqrt{x}\)
=>\(\sqrt{x}\in\left\{1;7\right\}\)
=>\(x\in\left\{1;49\right\}\)
b: ĐKXĐ: x>1
Để B là số nguyên thì \(3⋮\sqrt{x-1}\)
=>\(\sqrt{x-1}\in\left\{1;3\right\}\)
=>\(x-1\in\left\{1;9\right\}\)
=>\(x\in\left\{2;10\right\}\)
c: ĐKXĐ: x>3
Để C là số nguyên thì \(2⋮\sqrt{x-3}\)
=>\(\sqrt{x-3}\in\left\{1;2\right\}\)
=>\(x-3\in\left\{1;4\right\}\)
=>\(x\in\left\{4;7\right\}\)
Đúng 0
Bình luận (0)
Tìm x \(\in\) Z để:
\(\dfrac{3n-3}{3n-2}\) có giá trị là số nguyên.
`ĐK:n in Z`
`(3n-3)/(3n-2) in Z`
`=>3n-3 vdots 3n-2`
`=>3n-2-1 vdots 3n-2`
`=>1 vdots 3n-2`
`=>3n-1 in Ư(1)={1,-1}`
`+)3n-1=-1=>3n=0=>n=0(TM)`
`+)3n-1=1=>3n=2=>n=2/3`(loại).
Vậy `n=0` thì `A in Z`
Đúng 1
Bình luận (9)
Để \(\dfrac{3n-3}{3n-2}\) có giá trị là số nguyên thì \(3n-3⋮3n-2\)
\(\Leftrightarrow3n-2-1⋮3n-2\)
mà \(3n-2⋮3n-2\)
nên \(-1⋮3n-2\)
\(\Leftrightarrow3n-2\inƯ\left(-1\right)\)
\(\Leftrightarrow3n-2\in\left\{1;-1\right\}\)
\(\Leftrightarrow3n\in\left\{3;1\right\}\)
\(\Leftrightarrow n\in\left\{1;\dfrac{1}{3}\right\}\)
mà n nguyên
nên n=1
Vậy: Để \(\dfrac{3n-3}{3n-2}\) có giá trị là số nguyên thì n=1
Đúng 1
Bình luận (0)
Tìm x thuộc Z để biểu thức có giá trị nguyên: A=\(\dfrac{2\sqrt{x}+3}{3\sqrt{x}-1}\)
Để A nguyên thì \(2\sqrt{x}+3⋮3\sqrt{x}-1\)
\(\Leftrightarrow6\sqrt{x}+9⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;11\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;12\right\}\)
hay \(x\in\left\{0;16\right\}\)
Đúng 0
Bình luận (2)








