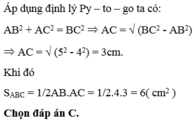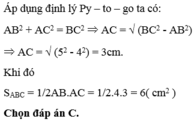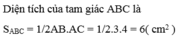Bài 7: Cho Δ ABC vuông tại A, có AB=9cm ; AC=12cm
a.Tính BC
b. Đường trung tuyến AM và đường trung tuyến BN cắt nhau tại G.Tính AG
c. Trên tia đối của tia NB, lấy điểm D sao cho NB=ND. Chứng minh CD⊥AC
Bài 8: Cho Δ MNP có MN<MP. Phân giác MD(D∈NP).Trên tia MP lấy điểm I sao cho MI=MN
a. Chứng minh DN=DI
b. Gọi K là giao điểm của đường thẳng MN và ID
Chứng minh ΔDNK=ΔDIP
GIúp mik vs nha
mik cảm ơn các bn trc