Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Biết HB= 4cm, HC= 9cm. Tính AB, AC,AH
TH
Những câu hỏi liên quan
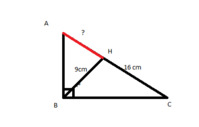
cho tam giác ABC vuông tại A .kẻ AH vuông góc với BC . biết HB = 9cm,HC =16 cm;AC=5cm . tính AH;AB
TA CÓ BH + HC = BC
=> BC = 9+16=25
THEO ĐỊNH LÝ PITAGO XÉT \(\Delta ABC\)VUÔNG TẠI A CÓ
\(BC^2=AB^2+AC^2\)
\(AB^2=BC^2-AC^2\)
\(AB^2=25^2-5^2\)
......
AH TƯƠNG TỰ
cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC)
a) biết HB = 4cm , HC = 9cm. tính AH và số đo góc ABC
b) gọi D là hình chiếu của H trên AB; E là hình chiếu của H trên AC. chứng minh CE.BD.AC.AB = AH4
c) kẻ AI vuông góc với ED (I thuộc BC). chứng minh I là trung điểm BC
giải chi tiết giúp mình ạ! mình cảm ơn nhiều<3
a/
\(AH^2=HB.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH=\sqrt{HB.HC}=\sqrt{4.9}=6cm\)
\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{6}{4}=\dfrac{3}{2}\)
b/
Xét tg vuông AHB có
\(HB^2=BD.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Xét tg vuông AHC có
\(HC^2=CE.AC\) (lý do như trên)
\(CE.BD.AC.AB=HB^2.HC^2=\left(HB.HC\right)^2\)
Mà \(HB.HC=AH^2\) (cmt)
\(\Rightarrow CE.BD.AC.AB=AH^4\)
c/
\(HD\perp AB;AC\perp AB\) => HD//AC => HD//AE
\(HE\perp AC;AB\perp AC\) => HE//AB => HE//AD
=> ADHE là hình bình hành mà \(\widehat{A}=90^o\) => ADHE là HCN
Xét tg vuông ADH và tg vuông ADE có
HD = AE (cạnh đối HCN)
AD chung
=> tg ADH = tg ADE (Hai tg vuông có 2 cạnh góc vuông = nhau)
\(\Rightarrow\widehat{AED}=\widehat{AHD}\)
\(\widehat{AHD}=\widehat{B}\) (cùng phụ với \(\widehat{BAH}\) )
\(\Rightarrow\widehat{AED}=\widehat{B}\) (1)
\(\widehat{C}+\widehat{B}=90^o\) (2)
\(\widehat{IAE}+\widehat{AED}=90^o\Rightarrow\widehat{IAE}+\widehat{B}=90^o\) (3)
Từ (2) và (3) => \(\widehat{IAE}=\widehat{C}\) => tg AIC cân tại I => IA=IC
Ta có
\(\widehat{IAE}+\widehat{BAI}=\widehat{A}=90^o\)
\(\Rightarrow\widehat{C}+\widehat{BAI}=90^o\) mà \(\widehat{C}+\widehat{B}=90^o\)
\(\Rightarrow\widehat{BAI}=\widehat{B}\) => tg ABI cân tại I => IA=IB
Mà IA= IC (cmt)
=> IB=IC => I là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC).Biết HB = 9cm, HC = 16cm. Tính độ dài AH.
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Biết HB = 9cm; HC = 16cm. Tính AH.
Help me
Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng hệ thức : AH^2 = HB . HC = 16 . 9
=> AH = 4 . 3 = 12 cm
Đúng 3
Bình luận (0)
Áp dụng hệ thức liên quan tới đường cao vào Δvuông ABC, ta được:
AH²= BH.CH = 9.16 = 144
⇒ AH=12 (cm)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại a có đường cao AH 1.cho biết AB =3cm , AC=4cm , tính độ dài các đoạn BC,HB,HC,AH 2. Kẻ HE vuông góc với AB , HF vuông góc với AC ( E thuộc AB , F thuộc AC )
a: BC=5cm
AH=2,4cm
BH=1,8cm
CH=3,2cm
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A .kẻ AH vuông góc với BC . biết HB = 9cm,HC =16 cm . tính AH
đề 1:
Cho tam giác ABC vuông tại A, AH vuông góc BC,AB=30cm,AH=24cm.
a)tính BH?BC?
b)tính các tỉ số lượng giác của các góc của tam giác AHB
đề 2
cho tam giác ABC vuông tại A, AH vuông góc BC , HB=4cm, HC=9cm
a)tính các cạnh tam giác ABC
b)tính các góc của tam giác ABC
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Biết AB=6cm,AC=8cm.Tính AH,HB,HC
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{10}=\dfrac{24}{5}cm\)
* Áp dụng hệ thức \(AB^2=HB.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
\(CH=BC-BH=10-\dfrac{18}{5}=\dfrac{32}{5}cm\)
Đúng 1
Bình luận (0)
bài này ko đủ dữ kiện. nếu bổ sung dữ kiện thì ta có thể tính dc với cách tính của định lý pitago.những bài này thường có 3 dữ kiện trở lên
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a đường cao ah trên bc lấy d khác h . tính ab ac ah biết hb=1.8 hc=3.2 .kẻ dm vuông góc với ab tại m dn vuông góc với ac tại n chứng minh bm.cn=dm.dn
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=1.8\cdot3.2=5.76\)
hay AH=2,4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=1.8\cdot5=9\\AC^2=3.2\cdot5=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=3\left(cm\right)\\AC=4\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Kẻ AH vuông góc với BC ( H thuộc BC). Biết AH = 12cm, HB =9cm, Hc = 20cm
a) Tính AB? AC?
b) Tam giác ABC có phải tam giác vuông không? Vì sao?






