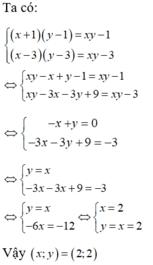(x+1)(xy-1)=3
TM
Những câu hỏi liên quan
rút gọn
1, 1/7 x^2 y^3 ( -14/3 xy^2 ) -1/2 xy ( x^2 y^4 )
2, ( 3xy )^2 ( -1/2 x^3 y^2 )
3) ( -1/4 x^2 y )^2 ( 2/3 xy^4)^3
1) Ta có: \(\dfrac{1}{7}x^2y^3\cdot\left(-\dfrac{14}{3}xy^2\right)\cdot\left(-\dfrac{1}{2}xy\right)\left(x^2y^4\right)\)
\(=\left(-\dfrac{1}{7}\cdot\dfrac{14}{3}\cdot\dfrac{-1}{2}\right)\left(x^2y^3\cdot xy^2\cdot xy\cdot x^2y^4\right)\)
\(=\dfrac{1}{3}x^6y^{10}\)
2) Ta có: \(\left(3xy\right)^2\cdot\left(-\dfrac{1}{2}x^3y^2\right)\)
\(=9xy^2\cdot\dfrac{-1}{2}x^3y^2\)
\(=-\dfrac{9}{2}x^4y^4\)
3) Ta có: \(\left(-\dfrac{1}{4}x^2y\right)^2\cdot\left(\dfrac{2}{3}xy^4\right)^3\)
\(=\dfrac{1}{16}x^4y^2\cdot\dfrac{8}{27}x^3y^{12}\)
\(=\dfrac{1}{54}x^7y^{14}\)
Đúng 0
Bình luận (0)
Tìm đa thức b biết
B-(3\(x^6\)-4\(xy^5\)+\(\dfrac{1}{3}\)\(xy^2\)-\(\dfrac{3}{2}\))=(7\(x^6\)-\(\dfrac{1}{2}xy^5-xy^2-\dfrac{1}{3}\))
B-(\(3x^6-4xy^5+\dfrac{1}{3}xy^2\))=
B= \(\left(7x^6-\dfrac{1}{2}xy^5-xy^2-\dfrac{1}{3}\right)+\left(3x^6-4xy^5+\dfrac{1}{3}xy^2-\dfrac{3}{2}\right)\)
B= \(7x^6-\dfrac{1}{2}xy^5-xy^2-\dfrac{1}{3}+3x^6-4xy^5+\dfrac{1}{3}xy^2-\dfrac{3}{2}\)
B= \(7x^6+3x^6-\dfrac{1}{2}xy^5-4xy^5-xy^2+\dfrac{1}{3}xy^2-\dfrac{1}{3}+\dfrac{2}{3}\)
B= \(10x^6-\dfrac{9}{2}xy^5-\dfrac{2}{3}xy^2+\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
(1/3x+2).(3x-6)
(x^2-3x+9).(x+3)
(-2xy+3).(xy-1)
x(xy-1).(xy+1)
\(\left(\frac{1}{3}x+2\right)\left(3x-6\right)\)
\(=\frac{1}{3}x\left(3x-6\right)+2\left(3x-6\right)\)
\(=x^2-2x+6x-12\)
\(=x^2+4x-12\)
\(\left(x^2-3x+9\right)\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-3x+9\right)\)
\(=x^3+27\)
a) (1/3x+2).(3x-6) = (1/3x.3x)+(1/3x.-6)+(2.3x)+(2.-6) = x^2-2x+6x-12 = x^2+4x-12 = x^2+2x2+2^2-16 = (x+2)^2-16
b) (x^2-3x+9).(x+3) = (x^2.x)+(x^2.3)+(-3x.x)+(-3x.3)+(9.x)+(9.3) = x^3+3x^2-3x^2-9x+9x+27 = x^3+27
c) (-2xy+3).(xy-1) = (-2xy.xy)+(-2xy.-1)+(3.xy)+(3.-1) = -2x^2y^2+2xy+3xy-3 = -2x^2y^2+5xy-3
d) x(xy-1).(xy+1) = (x^2y-x).(xy+1) = (x^2y.xy)+(x^2y.1)+(-x.xy)+(-x.1) = x^3y^2+x^2y-x^2y-x = x^3y^2-x
giải/hệ/phương/trình:(x+1)(y-1)=xy-1
(x-3)(y-3)=xy-3
\(\left\{{}\begin{matrix}\left(x+1\right)\left(y-1\right)=xy-1\\\left(x-3\right)\left(y-3\right)=xy-3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}xy-x+y-1=xy-1\\xy-3x-3y+9=xy-3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}-x+y=0\\-3x-3y=-12\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}-x+y=0\\x+y=4\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2y=4\\x+y=4\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=2\\x+2=4\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=2\\x=2\end{matrix}\right.\)
Vậy (2;2) là nghiệm
Đúng 1
Bình luận (2)
Cho xy khac 0 va x+y=1
Chung minh rang : x/y^3-1+y/x^3-1-2(xy-2)/(xy)^2+3=0
cho biểu thức: Pleft(frac{sqrt{x}+1}{sqrt{xy}+1}+frac{sqrt{xy}+sqrt{x}}{1-sqrt{xy}}+1right):left(1-frac{sqrt{xy}+sqrt{x}}{sqrt{xy}-1}-frac{sqrt{x}+1}{sqrt{xy}+1}right) Pleft(frac{sqrt{x}+1}{sqrt{xy}+1}+frac{sqrt{xy}+sqrt{x}}{1-sqrt{xy}}+1right):left(1-frac{sqrt{xy}+1}{sqrt{xy}-1}-frac{sqrt{x}+1}{sqrt{xy}+1}right).backslash với x,yge0;x,yne1 a) Rút gọn Pb) Tính P khi xsqrt[3]{4-2sqrt{6}}+sqrt[3]{4+2sqrt{6}}và yx^2+6
Đọc tiếp
cho biểu thức: \(P=\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+\sqrt{x}}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right)\) \(P=\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+1}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right).\backslash\ \)với \(x,y\ge0;x,y\ne1\)
a) Rút gọn P
b) Tính P khi \(x=\sqrt[3]{4-2\sqrt{6}}+\sqrt[3]{4+2\sqrt{6}}\)và \(y=x^2+6\)
a/ \(P=\frac{1}{\sqrt{xy}}\)
b/ \(x^3=8-6x\)
\(\Rightarrow P=\frac{1}{\sqrt{x\left(x^2+6\right)}}=\frac{1}{\sqrt{x^3+6x}}=\frac{1}{\sqrt{8-6x+6x}}=\frac{1}{2\sqrt{2}}\)
Đúng 0
Bình luận (0)
Thực hiện phép tính:a) M (x - 1)(x - 2)(x + 2) -
(
x
-
3
)
3
;b) N (xy - 1)(xy - 2) -
(
xy
-
2
)
2
.
Đọc tiếp
Thực hiện phép tính:
a) M = (x - 1)(x - 2)(x + 2) - ( x - 3 ) 3 ;
b) N = (xy - 1)(xy - 2) - ( xy - 2 ) 2 .
a) Chú ý: (x – 2)(x + 2) = x 2 – 4.
Khai triển M = x 3 – x 2 – 4x + 4 – ( x 3 – 9 x 2 + 27x – 27).
Rút gọn M = 8x2 + 31x + 31.
b) Đặt (xy – 2) làm nhân tử chung.
Rút gọn N = xy – 2.
Đúng 0
Bình luận (0)
Số nghiệm của hệ phương trình
(
x
+
1
)
(
y
-
1
)
x
y
-
1
(
x
-...
Đọc tiếp
Số nghiệm của hệ phương trình ( x + 1 ) ( y - 1 ) = x y - 1 ( x - 3 ) ( y - 3 ) = x y - 3 là
A. 1
B. 0
C. 2
D. Vô s
(căn x-căn y)/xy căn xy/((1/x+1/y)*1/(x+y+2 căn xy)+2/(căn x + căn y)^3*(1/ căn x+1/ căn y))v
\(a)\frac{{3{\rm{x}} - 1}}{{xy}} + \frac{{2{\rm{x}} - 1}}{{xy}}\)
\(b)\frac{{3{\rm{x}}}}{{{x^2} + 1}} + \frac{{ - 3{\rm{x}} + 1}}{{{x^2} + 1}}\)
\(a,\dfrac{3x-1}{xy}+\dfrac{2x-1}{xy}\\ =\dfrac{3x-1+2x-1}{xy}\\ =\dfrac{5x-2}{xy}\\ b,\dfrac{3x}{x^2+1}+\dfrac{-3x+1}{x^2+1}\\=\dfrac{3x-3x+1}{x^2+1}\\ =\dfrac{1}{x^2+1}\)
Đúng 1
Bình luận (0)