Vẽ đồ thị hàm số \(y=\dfrac{\left|2x\right|}{x}\)
TY
Những câu hỏi liên quan
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
a) khảo sát và vẽ đồ thị hàm số \(y=x^4-2x^2+3\)
b) vẽ đồ thị hàm số \(y=\left|x^4-2x^2+3\right|\)
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị là left(d_2right)
1) Với m 1
a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị là \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
Với m = 1
(d1) có dạng y = x + 3
(d2) có dạng y = -x + 3
Phương trình hoành độ giao điểm
-x + 3 = x + 3
<=> x = 0
Với x = 0 <=> y = 3
Tọa độ giao điểm A(0;3)
Đúng 1
Bình luận (0)
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị left(d_2right)1) Với m 1 a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: 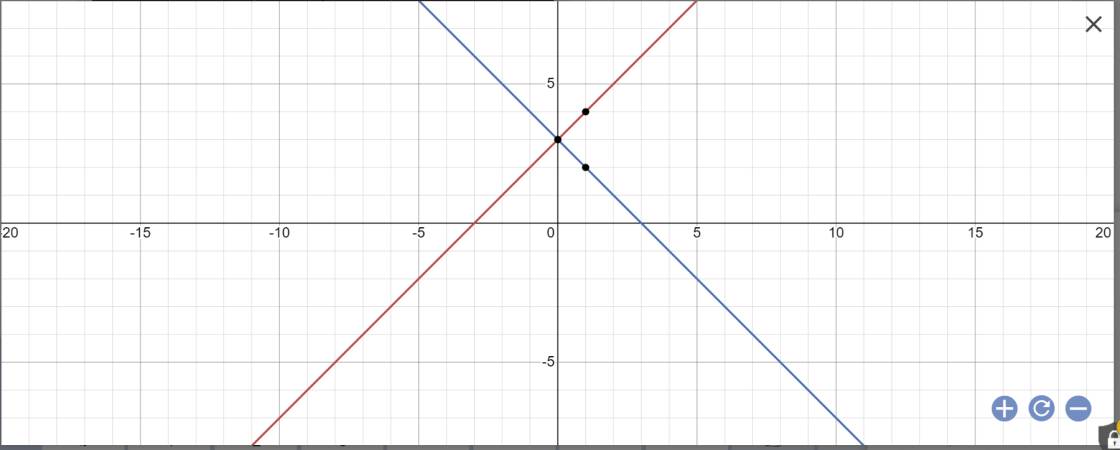
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3
Đúng 2
Bình luận (0)
Cho hàm số \(y=-\dfrac{5}{2}x\)
a) Xác định vị trí của điểm \(A\left(1,-\dfrac{5}{2}\right)\) trên mặt phẳng tọa độ , và vẽ đồ thị hàm số đó.
b) Xét xem trong các điểm sau , điểm nào thuộc đồ thị hàm số ? \(B\left(2,-5\right),C\left(3,7\right),D\left(l,\dfrac{5}{2}\right),E\left(0,4\right)\)
a: Thay x=1 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)
Vậy: \(A\left(1;-\dfrac{5}{2}\right)\) thuộc đồ thị hàm số y=-5/2x
b: Thay x=2 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot2=-5\)
=>B(2;-5) thuộc đồ thị hàm số y=-5/2x
Thay x=3 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot3=-\dfrac{15}{2}\)<>7
=>\(C\left(3;7\right)\) không thuộc đồ thị hàm số y=-5/2x
Thay x=1 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)<>5/2
=>\(D\left(1;\dfrac{5}{2}\right)\) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)
Thay x=0 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot0=0\)<>4
=>E(0;4) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)
Đúng 1
Bình luận (0)
vẽ đồ thị của hàm số sau
a) \(y=3^x\)
b) \(y=\left(\dfrac{1}{2}\right)^x\)
a: Bảng giá trị:
| x | 1 | 2 | 3 |
| \(y=3^x\) | 3 | 9 | 27 |
Vẽ đồ thị:
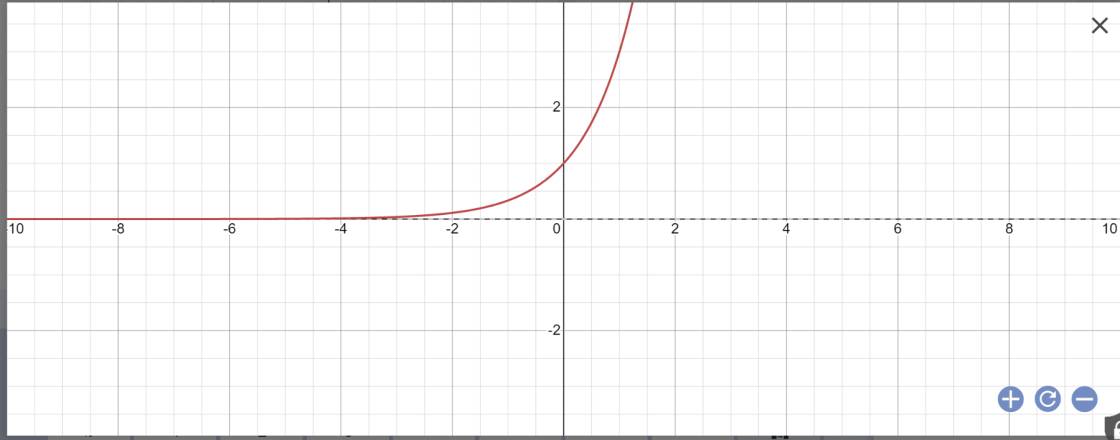
b: Bảng giá trị:
| x | 2 | 3 | 4 |
| \(y=\left(\dfrac{1}{2}\right)^x\) | 1/4 | 1/8 | 1/16 |
vẽ đồ thị:
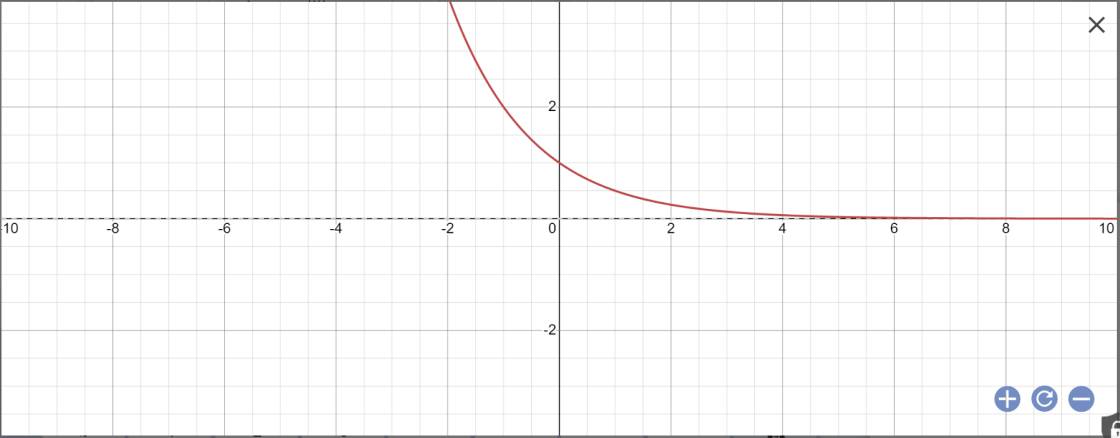
Đúng 1
Bình luận (0)
Cho hàm số :
\(y=f\left(x\right)=\left\{{}\begin{matrix}\dfrac{2}{3}x^2-\dfrac{8}{3}x+2;\left(x>0\right)\\2x+2;\left(x\le0\right)\end{matrix}\right.\)
Vẽ đồ thị của hàm số \(y=\left|f\left(x\right)\right|\) ?
Vẽ đồ thị các hàm số :
a. \(y=\left\{{}\begin{matrix}2x;\left(x\ge0\right)\\-\dfrac{1}{2}x;\left(x< 0\right)\end{matrix}\right.\)
b. \(y=\left\{{}\begin{matrix}x+1;\left(x\ge1\right)\\-2x+4;\left(x< 1\right)\end{matrix}\right.\)
Vẽ đồ thị hàm số :
\(y=\left\{{}\begin{matrix}2x-1;\left(x\ge1\right)\\\dfrac{1}{2}x+1;\left(x< 1\right)\end{matrix}\right.\)

Điểm \(\left(1;1\right)\) thuộc đồ thị, điểm \(\left(1;\dfrac{3}{2}\right)\) không thuộc đồ thị .
Đúng 0
Bình luận (0)
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\) có đường tiệm cận ngang đi qua điểm M (-2;1)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = 1
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1
Đúng 1
Bình luận (0)







