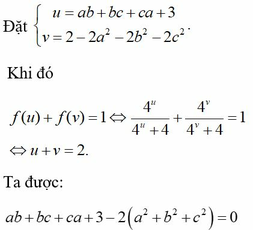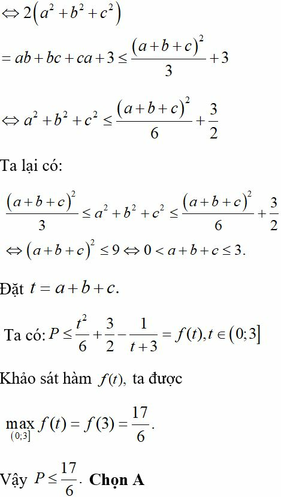Cho a,b,c thực thõa mãn a2+2b2+5c2=22.Tìm GTLN của biểu thức A=ab+ac+bc
HC
Những câu hỏi liên quan
Cho a,b,c thực thõa mãn a2+2b2+5c2=22.Tìm GTLN của biểu thức A=ab+ac+bc
Áp dụng BĐT AM-GM ta có:
\(\frac{2}{3}a^2+\frac{3}{2}b^2\ge2ab\)
\(\frac{b^2}{2}+2c^2\ge2bc\)
\(3c^2+\frac{a^2}{3}\ge2ac\)
\(\Rightarrow2A\le a^2+2b^2+5c^2=22\Rightarrow A\le11\)
\("="\Leftrightarrow a=3;b=2;c=1\)
Đúng 0
Bình luận (0)
Cho a, b, c là số thực dương thỏa mãn: a+b+c=1. Tìm GTLN của biểu thức: \(P=\sqrt{\dfrac{ab}{c+ab}}+\sqrt{\dfrac{bc}{a+bc}}+\sqrt{\dfrac{ac}{b+ac}}\)
Lời giải:
Áp dụng BĐT AM-GM:
\(P=\sum \sqrt{\frac{ab}{c+ab}}=\sum \sqrt{\frac{ab}{c(a+b+c)+ab}}=\sum \sqrt{\frac{ab}{(c+a)(c+b)}}\)
\(\leq \sum \frac{1}{2}\left(\frac{a}{c+a}+\frac{b}{c+b}\right)=\frac{1}{2}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}\right)=\frac{3}{2}\)
Vậy $P_{\max}=\frac{3}{2}$ khi $a=b=c=\frac{1}{3}$
Đúng 2
Bình luận (0)
cho a, b,c >0 thỏa mãn ab+bc+ca=abc
CMR : (√b2+2a2)/ab + (√c2+2b2)/bc + (√a2+2c2)/ac
cho ΔABC có AB=c, BC=a, CA=b. diện tích ΔABC là 5 cm2. tìm GTNN của biểu thức a2+2b2+3c2
Cho 3 số thực không âm a, b, c thỏa mãn a2 + b2 + c2 = 1. Tìm giá trị lớn nhất của biểu thức T = a + b2011 + c1954 – ab – bc – ac.
Do \(a^2+b^2+c^2=1\Rightarrow0\le a;b;c\le1\)
\(\Rightarrow\left\{{}\begin{matrix}\left(a-1\right)\left(b-1\right)\left(c-1\right)\le0\\b^{2011}\le b\\c^{2011}\le c\end{matrix}\right.\)
\(\Rightarrow T\le a+b+c-ab-bc-ca=\left(a-1\right)\left(b-1\right)\left(c-1\right)+1-abc\le1-abc\le1\)
\(T_{max}=1\) khi \(\left(a;b;c\right)=\left(0;0;1\right)\) và các hoán vị
Đúng 0
Bình luận (0)
cho tam giác ABC có BC=a, AB = c , AC=b thỏa mãn hệ thức a2 +b2 =5c2 , tính góc giữa 2 trung tuyến AM và BN
Gọi G là giao điểm của AM và BN.
Theo công thức tính độ dài đường trung tuyến: \(AM^2=\dfrac{2b^2+2c^2-a^2}{4}\);
\(BN^2=\dfrac{2c^2+2a^2-b^2}{4}\).
Từ đó \(AG^2=\dfrac{4}{9}AM^2=\dfrac{2b^2+2c^2-a^2}{9}\); \(BG^2=\dfrac{4}{9}BN^2=\dfrac{2c^2+2a^2-b^2}{9}\).
Do đó \(AG^2+BG^2=\dfrac{a^2+b^2+4c^2}{9}=\dfrac{9c^2}{9}=c^2=AB^2\).
Theo định lý Pythagoras đảo thì tam giác AGB vuông tại G.
Vậy góc giữa 2 trung tuyến AM và BN là 90o.
Đúng 5
Bình luận (0)
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4
Cho 3 số thực dương a, b, c thõa mãn a + b + c = 1. Tìm GTLN của biểu thức
\(A=\sqrt{2ab+2b} + \sqrt{2bc+2c} + \sqrt{2ca+2a}\)
\(A=\sqrt{2b\left(a+1\right)}+\sqrt{2c\left(b+1\right)}+\sqrt{2a\left(c+1\right)}\)
\(A=\dfrac{1}{2\sqrt{2}}.2\sqrt{4b\left(a+1\right)}+\dfrac{1}{2\sqrt{2}}.2\sqrt{4c\left(b+1\right)}+\dfrac{1}{2\sqrt{2}}.2\sqrt{4a\left(c+1\right)}\)
\(A\le\dfrac{1}{2\sqrt{2}}\left(4b+a+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4a+c+1\right)\)
\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
a,b,b là các số thực dương thỏa mãn a+b+c=3
Tìm GTLN của biểu thức P = 2(ab+bc+ac) - abc
\(a=b=c=1\rightarrow P=5\)ta se cm P=5 la gtln cua P that vay ta se cm
\(5p^3+27r\ge18pq\Leftrightarrow5p^3+27r-18pq\ge0\).theo bdt schur
\(LHS\ge5p^3+3p\left(4q-p^2\right)-18pq=2p\left(p^2-3q\right)\ge0\)
Vay \(P_{max}=5\leftrightarrow a=b=c=1\)
Đúng 0
Bình luận (0)
Đặt P = F(a;b;c).
Xét hiệu \(F\left(a;b;c\right)-F\left(t;t;c\right)=2\left(ab+bc+ca-t^2-2tc\right)+c\left(t^2-ab\right)\)
\(=2\left(ab-t^2\right)-c\left(ab-t^2\right)+2c\left(a+b-2t\right)\)
\(=2\left(ab-t^2\right)-c\left(ab-t^2\right)\)
\(=\left(ab-t^2\right)\left(2-c\right)\le0\) với \(t=\frac{a+b}{2}\). Do đó \(f\left(a;b;c\right)\le f\left(t;t;c\right)\)
Ta sẽ chứng minh \(f\left(t;t;c\right)\le5\) hay \(2\left(t^2+2tc\right)-t^2c\le5\)
\(\Leftrightarrow\left(2-c\right)t^2+4tc-5\le0\). Thật vậy từ giả thiết suy ra \(c=3-2t\).Mặt khác do c > 0 và t > 0 nên \(0< t< \frac{3}{2}\)
Do đó ta cần chứng minh \(\left(2t-1\right)t^2+4t\left(3-2t\right)-5\le0\) với \(0< t< \frac{3}{2}\)
\(\Leftrightarrow\left(t-1\right)^2\left(2t-5\right)\le0\). BĐT này đúng với mọi \(0< t< \frac{3}{2}\)
P/s: Is it true?? Em mới học dồn biến nên ko chắc đâu..
Đúng 0
Bình luận (0)
Xem thêm câu trả lời