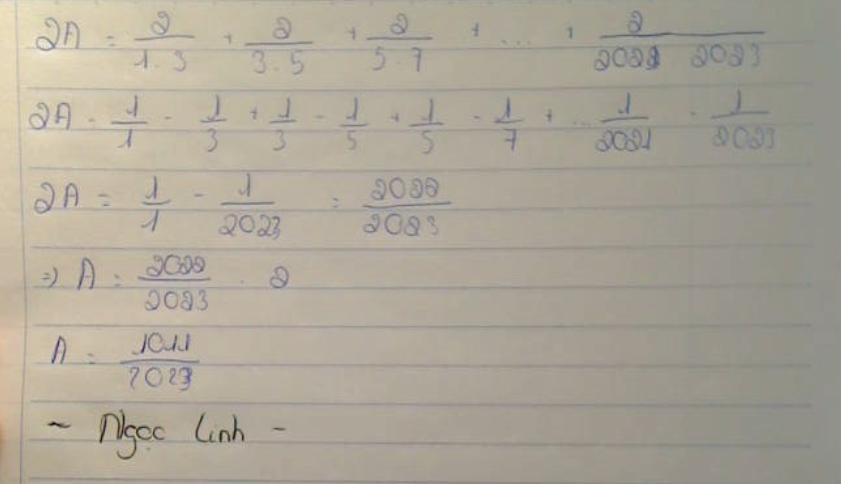Tính tổng: \(S=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2007.2009}\)
QL
Những câu hỏi liên quan
TÍNH TỔNG
S= \(\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{3.5}\right)\left(1+\dfrac{1}{5.7}\right)...(1+\dfrac{1}{2007.2009})\)
I.Tìm các giá trị nguyên để biểu thức \(\dfrac{3n+4}{n+2}\) là số nguyên.
II. Cho biểu thức A=\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{2007.2009}\)
So sánh D với \(\dfrac{2009}{4019}\)
I: Để 3n+4/n+2 là số nguyên thì \(3n+4⋮n+2\)
\(\Leftrightarrow3n+6-2⋮n+2\)
\(\Leftrightarrow n+2\in\left\{1;-1;2;-2\right\}\)
hay \(n\in\left\{-1;-3;0;-4\right\}\)
II: \(D=2\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2007}-\dfrac{1}{2009}\right)\)
\(D=2\cdot\left(1-\dfrac{1}{2009}\right)=2\cdot\dfrac{2008}{2009}=\dfrac{4016}{2009}\)
Đúng 2
Bình luận (0)
tính tổng có quy luật :
H=\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+......+\(\dfrac{1}{47.49}\)+\(\dfrac{1}{49.51}\)
\(2H=\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{49.51}\)
\(2H=\dfrac{3-1}{1.3}+\dfrac{5-3}{3.5}+...+\dfrac{51-49}{49.51}\)
\(2H=\dfrac{3}{1.3}-\dfrac{1}{1.3}+\dfrac{5}{3.5}-\dfrac{3}{3.5}+...+\dfrac{51}{49.51}-\dfrac{49}{49.51}\)
\(2H=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{49}-\dfrac{1}{51}\)
\(2H=1-\dfrac{1}{51}\)
\(2H=\dfrac{50}{51}\)
\(H=\dfrac{25}{51}\)
Đúng 1
Bình luận (0)
tính tổng các phân số sau:
a)\(\dfrac{1}{1.2}\)+\(\dfrac{1}{2.3}\)+\(\dfrac{1}{3.4}\)+❓+\(\dfrac{1}{2003.2004}\)
b)\(\dfrac{1}{1.3}\)+\(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+❓\(\dfrac{1}{2003.2005}\)
a) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2003.2004}=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2003}-\dfrac{1}{2004}=1-\dfrac{1}{2004}=\dfrac{2003}{2004}\)b)Đặt \(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2003.2005}\)
\(\Rightarrow2A=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{2003.2005}=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2003}-\dfrac{1}{2005}=1-\dfrac{1}{2005}=\dfrac{2004}{2005}\)\(\Rightarrow A=\dfrac{1002}{2005}\)
Đúng 1
Bình luận (0)
a: Ta có: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2003\cdot2004}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2003}-\dfrac{1}{2004}\)
\(=\dfrac{2003}{2004}\)
Đúng 1
Bình luận (0)
b: Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{2003\cdot2005}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{2003\cdot2005}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2003}-\dfrac{1}{2005}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2004}{2005}=\dfrac{1002}{2005}\)
Đúng 1
Bình luận (0)
Tính tổng
\(S=\dfrac{1}{1.3}-\dfrac{1}{2.4}+\dfrac{1}{3.5}-\dfrac{1}{4.6}+\dfrac{1}{5.7}-\dfrac{1}{6.8}+\dfrac{1}{7.9}-\dfrac{1}{8.10}\)
\(S=\dfrac{1}{1.3}-\dfrac{1}{2.4}+\dfrac{1}{3.5}-\dfrac{1}{4.6}+\dfrac{1}{5.7}-\dfrac{1}{6.8}+\dfrac{1}{7.9}-\dfrac{1}{8.10}\)
\(S=\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+\dfrac{1}{7.9}\right)-\left(\dfrac{1}{2.4}+\dfrac{1}{4.6}+\dfrac{1}{6.8}+\dfrac{1}{8.10}\right)\)
\(S=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{7}-\dfrac{1}{9}\right)-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{8}-\dfrac{1}{10}\right)\)
\(S=\dfrac{1}{2}-\dfrac{1}{18}-\dfrac{1}{4}+\dfrac{1}{20}\)
\(S=.C.A.S.I.O.\)
Đúng 0
Bình luận (0)
tính tổng \(S=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{\left(2n-1\right)\left(2n+1\right)}\)
\(S=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{\left(2n-1\right)\left(2n+1\right)}\)
\(\Rightarrow2S=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{\left(2n-1\right)\left(2n+1\right)}\)
\(\Rightarrow2S=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\) \(\Rightarrow2S=1-\dfrac{1}{2n+1}\)
\(\Rightarrow S=\dfrac{n}{2n+1}\)
Đúng 0
Bình luận (0)
Ta có : \(\dfrac{1}{\left(2n-1\right)\left(2n+1\right)}=\dfrac{1}{2}\left(\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right)\)
ta được \(\dfrac{1}{1.3}=\dfrac{1}{2}\left(\dfrac{1}{1}-\dfrac{1}{3}\right);\dfrac{1}{3.5}=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}\right);\dfrac{1}{5.7}=\dfrac{1}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}\right)\)
\(\dfrac{1}{\left(2n-1\right)\left(2n+1\right)}=\dfrac{1}{2}\left(\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right)\) vậy \(S=\dfrac{1}{2}\left(1-\dfrac{1}{2n+1}\right)=\dfrac{n}{2n+1}\)
Đúng 0
Bình luận (0)
Tính
\(\dfrac{1}{1.3}\)+ \(\dfrac{1}{3.5}\)+\(\dfrac{1}{5.7}\)+...+\(\dfrac{1}{2021.2023}\)
Ta có :
\(\dfrac{1}{1.3}\text{=}2\left(\dfrac{1}{1}-\dfrac{1}{3}\right)\)
\(\dfrac{1}{3.5}\text{=}2\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\)
\(\dfrac{1}{5.7}\text{=}2\left(\dfrac{1}{5}-\dfrac{1}{7}\right)\)
\(...\)
\(\dfrac{1}{2021.2023}\text{=}2\left(\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(\Rightarrow\) biểu thức chỉ còn :
\(2.1-\dfrac{2}{2023}\text{=}\dfrac{4044}{2023}\)
Đúng 3
Bình luận (0)
đặt biểu thức trên là A
ta có
2A=2/1.3+2/3.5+...+2/2021.2023
2A=1/1-1/3+1/3-1/5+...+1/2021-1/2023
2A=1/1-1/2023
2A=2022/2023
A=(2022/2023):2
A=1011/2023
Đúng 3
Bình luận (0)
Thực hiện phép tính ( tính hợp lý nếu có thể)
\(1-\dfrac{2}{1.3}-\dfrac{2}{3.5}-..\dots-\dfrac{2}{2021.2023}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tính
\(B=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)
\(B=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)
\(B=\dfrac{1}{1}\cdot\dfrac{1}{3}+\dfrac{1}{3}\cdot\dfrac{1}{5}+\dfrac{1}{5}\cdot\dfrac{1}{7}+...+\dfrac{1}{97}\cdot\dfrac{1}{99}\)
\(B=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)
\(B=\dfrac{1}{1}-\dfrac{1}{99}\)
\(B=\dfrac{99}{99}-\dfrac{1}{99}\)
\(B=\dfrac{98}{99}\)
#YVA
Đúng 1
Bình luận (0)
B=\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)
B=\(\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{97.99}\right):2\)
B=\(\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{97}-\dfrac{1}{99}\right):2\)
B=\(\left(\dfrac{1}{1}-\dfrac{1}{99}\right):2\)
B=\(\dfrac{98}{99}:2\)
B=\(\dfrac{49}{99}\)
Đúng 0
Bình luận (0)
Tính nhanh:
\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2021.2023}\)
\(A=1.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{5}+...+\dfrac{1}{2021}.\dfrac{1}{2023}=1-\dfrac{1}{2023}=\dfrac{2022}{2023}\)
Đúng 1
Bình luận (0)
\(A=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2022}{2023}=\dfrac{1011}{2023}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời