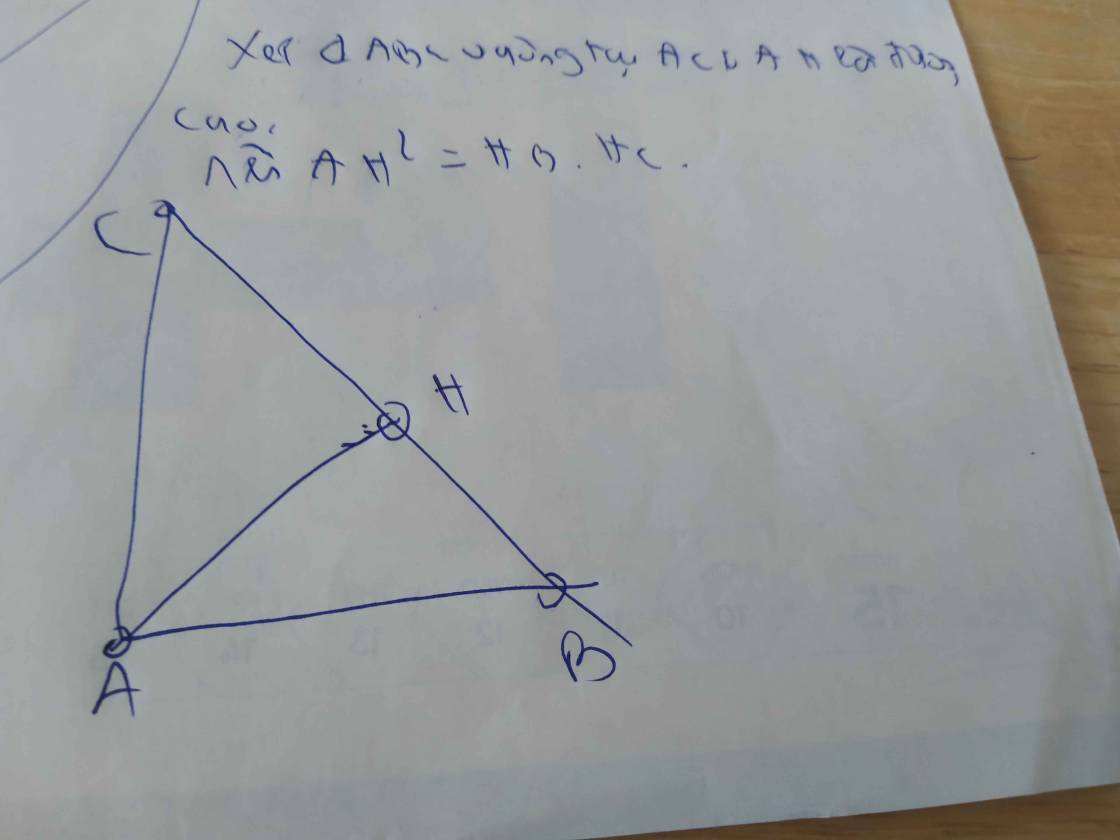
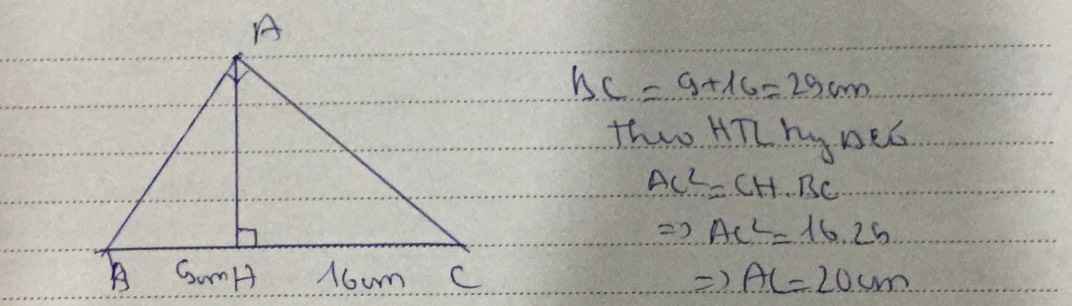Cho tam giác ABC vuông tại A , AH vuông góc với BC ( H thuộc BC ) . CM : AH2 = BH . HC
HH
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH2 = BH x HC
Cho tam giác ABC vuông tại A , AH vuông góc với BC ( H thuộc BC ) . CM : \(^{AH^2}\) = BH . HC
Cho tam giác ABC, góc A = 900, AH vuông góc BC, AB = 6cm, AC = 8 cm, phân giác của góc B cắt AH tại I, cắt BC tại D
1. Tính BC, AD, DC
2. CM tam giác ABC đồng dạng với tam giác HBA, tam giác ABI đồng dạng với tam giác CBD
3. CM AB2 = BH . BC, AH2 = HB . HC, \(\dfrac{IH}{IA}\) = \(\dfrac{AD}{BC}\)
1: BC=10cm
Xét ΔABC có BD là đường phân giác
nên AD/AB=DC/BC
=>AD/6=DC/10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3(cm); BD=5(cm)
2: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)
\(\widehat{IAB}=\widehat{DCB}\)
Do đó: ΔABI\(\sim\)ΔCBD
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH.
1) Cho biết AB=3 cm, AC=4 cm. Tính độ dài các đoạn BC,HB,HC,AH
2) Vẽ HE vuông góc với AB, HF vuông góc với AC (E thuộc AB, F thuộc AC)
Chứng minh: AE.EB+AF.FC=AH2
3) Chứng minh: BE=BC. cos3 B
1: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>BC=5(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=2,4(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\CH\cdot CA=CA^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1,8\left(cm\right)\\CH=\dfrac{4^2}{5}=3,2\left(cm\right)\end{matrix}\right.\)
2: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot EB=HE^2\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot FC=HF^2\)
\(AE\cdot EB+AF\cdot FC=HE^2+HF^2=EF^2=AH^2\)
3: Xét ΔBAC vuông tại B có \(cosB=\dfrac{BA}{BC}\)
Xét ΔBHA vuông tại H có \(cosB=\dfrac{BH}{BA}\)
Xét ΔBEH vuông tại E có \(cosB=\dfrac{BE}{BH}\)
\(cos^3B=cosB\cdot cosB\cdot cosB\)
\(=\dfrac{BA}{BC}\cdot\dfrac{BH}{BA}\cdot\dfrac{BE}{BH}=\dfrac{BE}{BC}\)
=>\(BE=BC\cdot cos^3B\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A có AB = AC = 5cm, kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: BH = HC và góc BAH = góc CAH
b) Tính độ dài BH biết AH = 4cm.
c) Kẻ HD vuông góc với AB (D thuộc AB), kẻ EH vuông góc với AC (E thuộc AC). Tam giác ADE là tam giác gì ? Vì sao ?
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Vẽ AH vuông góc với BC, H thuộc BC. Cho BH=9 cm, CH=16 cm. Tính AC
BC=BH+CH=25(cm)
\(AC=\sqrt{CH\cdot BC}=20\left(cm\right)\)
Đúng 1
Bình luận (0)
ta có:
\(AC^2=CH.BC\)
\(\Leftrightarrow AC=\sqrt{16.\left(16+9\right)}=\sqrt{400}=20cm\)
Đúng 1
Bình luận (0)
cho tam giác cân ABC có ABC : AB=AC=10cm , BC=12cm , gọi AH là tia phân giác góc A (H thuộc BC)
a. CM BH=HC và AH vuông góc BC
b. Tính độ dài AH
c. Kẻ HD vuông góc AB (D thuộc AB) HE vuông góc AC (E thuộc AC).Hỏi tam giác DHE là tam giác gì ?
d. CM DE//BC
Giúp mình với ạ 😭✨
a: ΔABC cân tại A có AH là phân giác
nên H là trung điểm của BC
ΔABC cân tại A có AH là trung tuyến
nên AH vuông góc BC
b: BH=CH=12/2=6cm
AH=căn AB^2-AH^2=8cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>AD=AE và HD=HE
=>ΔHDE cân tại H
d: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Kẻ AH vuông góc BC(H thuộc Bc).Tính độ dài AH,Biết BH=2cm,HC=8cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=2\cdot8=16\)
hay AH=4(cm)
Vậy: AH=4cm
Đúng 1
Bình luận (1)
cho tam giác abc vuống góc A, AH vuông BC(H thuộc BC)
a, chứng minh tam giác abc đồng dạng ới tam giác hba => Ab bình = BH . BC
b, CM tam giác abc đồng dạng với tam giác hac => Ac bình = CH . BC
c,CM AB . AC=AH .BC
d, CM AH bình =HB . HC
a) Xét \(\Delta ABC\) và \(\Delta HBA\) có \(\widehat{BAC}=\widehat{BHA}=90^o;\widehat{B}-\text{góc chung}\)
\(\Rightarrow \Delta ABC\sim\Delta HBA(g.g)\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{BA}\Rightarrow AB^2=BH.BC\)
Đúng 1
Bình luận (0)
b) Tương tự câu a
c) Ta có \(AB.AC=2S_{ABC}=AH.BC\)
Đúng 0
Bình luận (0)
d) Một cách cm lớp 7:
Theo định lý Pytago ta có \(AH^2+BH^2+AH^2+CH^2=AB^2+AC^2=BC^2=\left(BH+CH\right)^2\Leftrightarrow2AH^2=2BH.CH\Leftrightarrow AH^2=BH.CH\).
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC( H thuộc BC). Tính độ dài AH biết HB=2 cm, HC=8 cm