1) Giai
a) Sinx = 1
1) Giai
a) cos6x + sin6x
1) Giai
a) Sin ( x+\(\dfrac{\Pi}{3}\)) = 1
b) Sin ( x+\(\dfrac{\Pi}{3}\)) = -1
\(a,\sin\left(x+\dfrac{\pi}{3}\right)=1\\ \Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\\ \Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
giaia iguerm rem 
a) Áp dụng BĐT AM-GM, ta có:
\(VT\ge\dfrac{4xy}{2}+\dfrac{x}{4}+\dfrac{y}{4}=xy+\dfrac{x}{4}+xy+\dfrac{y}{4}\ge2\sqrt{xy.\dfrac{y}{4}}+2\sqrt{xy.\dfrac{x}{4}}=x\sqrt{y}+y\sqrt{x}\)
Vậy ta có đpcm.
c)
ta có : \(\dfrac{1}{1+x}\ge1-\dfrac{1}{1+y}+1-\dfrac{1}{1+z}=\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
Áp dụng bất đẳng thức AM - GM :
\(\Rightarrow\dfrac{1}{1+x}\ge\dfrac{y}{y+1}+\dfrac{z}{z+1}\ge2\sqrt{\dfrac{yz}{\left(y+1\right)\left(z+1\right)}}\)
tương tự ta cũng có
\(\dfrac{1}{1+y}\ge2\sqrt{\dfrac{xz}{\left(x+1\right)\left(z+1\right)}}\) ; \(\dfrac{1}{1+z}\ge2\sqrt{\dfrac{xy}{\left(x+1\right)\left(y+1\right)}}\)
nhân ba vế bất đẳng thức lại với nhau ta được
\(\dfrac{1}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\ge8\sqrt{\dfrac{x^2y^2z^2}{\left(x+1\right)^2\left(y+1\right)^2\left(z+1\right)^2}}\)
\(\Rightarrow\dfrac{1}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\ge\dfrac{8xyz}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(\Rightarrow xyz\le\dfrac{1}{8}\) \(\Rightarrow Max\left(xyz\right)=\dfrac{1}{8}\) khi \(x=y=z=\dfrac{1}{2}\)
\(\sqrt{\dfrac{1+sinx}{1-sinx}}+\sqrt{\dfrac{1-sinx}{1+sinx}}=?\) (sao cho gọn nhất)
\(=\dfrac{1+sinx+1-sinx}{\sqrt{\left(1-sinx\right)\left(1+sinx\right)}}=\dfrac{2}{\sqrt{1-sin^2x}}=\dfrac{2}{\sqrt{cos^2x}}=\dfrac{2}{\left|cosx\right|}\)
Rút gọn \(\sqrt{\frac{1+sinx}{1-sinx}}+\sqrt{\frac{1-sinx}{1+sinx}}\)
\(\sqrt{\frac{1+sinx}{1-sinx}}+\sqrt{\frac{1-sinx}{1+sinx}}=\sqrt{\frac{sin^2\frac{x}{2}+cos^2\frac{x}{2}+2sin\frac{x}{2}.cos\frac{x}{2}}{sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}.cos\frac{x}{2}}}+\sqrt{\frac{sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}.cos\frac{x}{2}}{sin^2\frac{x}{2}+cos^2\frac{x}{2}+2sin\frac{x}{2}.cos\frac{x}{2}}}\)
\(=\sqrt{\frac{\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2}{\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2}}+\sqrt{\frac{\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2}{\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2}}=\frac{\left|sin\frac{x}{2}+cos\frac{x}{2}\right|}{\left|sin\frac{x}{2}-cos\frac{x}{2}\right|}+\frac{\left|sin\frac{x}{2}-cos\frac{x}{2}\right|}{\left|sin\frac{x}{2}+cos\frac{x}{2}\right|}\)
\(=\frac{\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2+\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2}{\left|sin^2\frac{x}{2}-cos^2\frac{x}{2}\right|}=\frac{2}{\left|cosx\right|}\)
1, Tìm txd của hàm số sau
a, y = \(\sqrt{sinx-1}\)
b, y =\(\sqrt{\dfrac{1-sinx}{1+sinx}}\)
c, y = \(\dfrac{1+cosx}{sinx}\)
ĐKXĐ: (tất cả \(k\in Z\))
a. \(sinx-1\ge0\Leftrightarrow sinx\ge1\)
\(\Leftrightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b. \(\left\{{}\begin{matrix}\dfrac{1-sinx}{1+sinx}\ge0\left(luôn-đúng\right)\\1+sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx\ne-1\)
\(\Leftrightarrow x\ne-\dfrac{\pi}{2}+k2\pi\)
c. \(sinx\ne0\Leftrightarrow x\ne k\pi\)
Giải các phương trình sau:
a, \(\dfrac{Sin^2x+Sinx}{Sinx-1}=-2\)
b,\(\dfrac{Cos2x+Sinx}{Sinx-1}+1=0\)
a)Đk:\(sinx\ne1\)
Pt\(\Leftrightarrow sin^2x+sinx=-2\left(sinx-1\right)\)
\(\Leftrightarrow sin^2x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{-3+\sqrt{17}}{2}\left(tm\right)\\sinx=\dfrac{-3-\sqrt{17}}{2}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\\x=\pi-arc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\end{matrix}\right.\)(\(k\in Z\))
b)Đk:\(sinx\ne1\)
Pt \(\Leftrightarrow\dfrac{1-2sin^2x+sinx}{sinx-1}+1=0\)
\(\Leftrightarrow\dfrac{-\left(sinx-1\right)\left(2sinx+1\right)}{sinx-1}+1=0\)
\(\Leftrightarrow-\left(2sinx+1\right)+1=0\)
\(\Leftrightarrow sinx=0\) (tm)
\(\Leftrightarrow x=k\pi,k\in Z\)
Vậy...
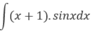 bằng:
bằng:
A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + C
C. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Đáp án: B.
Hướng dẫn: Đặt u = (x + 1), v' = sinx.
Cmr:
1) (Sinx)/(1+cosx)+(1+cosx)/sinx=2/sinx
2) cosx/(1-sinx)=cot(bi/4-x/2)
\(\frac{sinx}{1+cosx}+\frac{1+cosx}{sinx}=\frac{sin^2x+\left(1+cosx\right)^2}{sinx\left(1+cosx\right)}=\frac{sin^2x+cos^2x+2cosx+1}{sinx\left(1+cosx\right)}\)
\(=\frac{2+2cosx}{sinx\left(1+cosx\right)}=\frac{2\left(1+cosx\right)}{sinx\left(1+cosx\right)}=\frac{2}{sinx}\)
\(\frac{cosx}{1-sinx}=\frac{cos2.\frac{x}{2}}{1-sin2.\frac{x}{2}}=\frac{cos^2\frac{x}{2}-sin^2\frac{x}{2}}{sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}.cos\frac{x}{2}}=\frac{\left(cos\frac{x}{2}-sin\frac{x}{2}\right)\left(cos\frac{x}{2}+sin\frac{x}{2}\right)}{\left(cos\frac{x}{2}-sin\frac{x}{2}\right)^2}\)
\(=\frac{sin\frac{x}{2}+cos\frac{x}{2}}{cos\frac{x}{2}-sin\frac{x}{2}}=\frac{\sqrt{2}cos\left(\frac{\pi}{4}-\frac{x}{2}\right)}{\sqrt{2}sin\left(\frac{\pi}{4}-\frac{x}{2}\right)}=cot\left(\frac{\pi}{4}-\frac{x}{2}\right)\)