Càng chi tiết càng tốt ạ
SG
Những câu hỏi liên quan
càng chi tiết càng tốt ạ
39 D
40 D
41 B
42 C
43 C
44 B
45 D
46 B
47 C
48 B
49 B
50 C
Đúng 1
Bình luận (3)
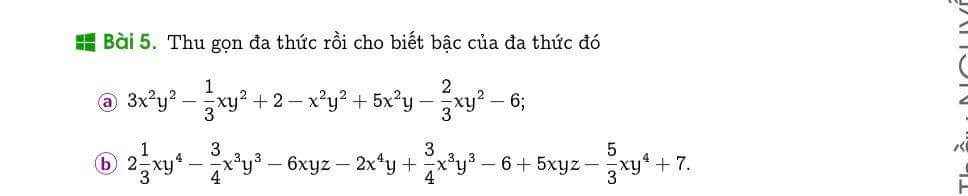 Cứu mik với, mik cảm ơn
Cứu mik với, mik cảm ơn
(càng chi tiết càng tốt ạ )
a, \(=2x^2y^2-xy^2-4+5x^2y\)
-> bậc 4
b, \(=\dfrac{2}{3}xy^4-xyz-2x^4y+1\)
-> bậc 5
Đúng 1
Bình luận (0)
Children must / have to start school when they are five.
gt với ạ càng chi tiết càng tốt
Children must / have to start school when they are five.
Đúng 0
Bình luận (1)
 chi tiết vẽ hình càng tốt ạ
chi tiết vẽ hình càng tốt ạ
Cần gấp ạ,chi tiết 1 chút càng tốt ạ.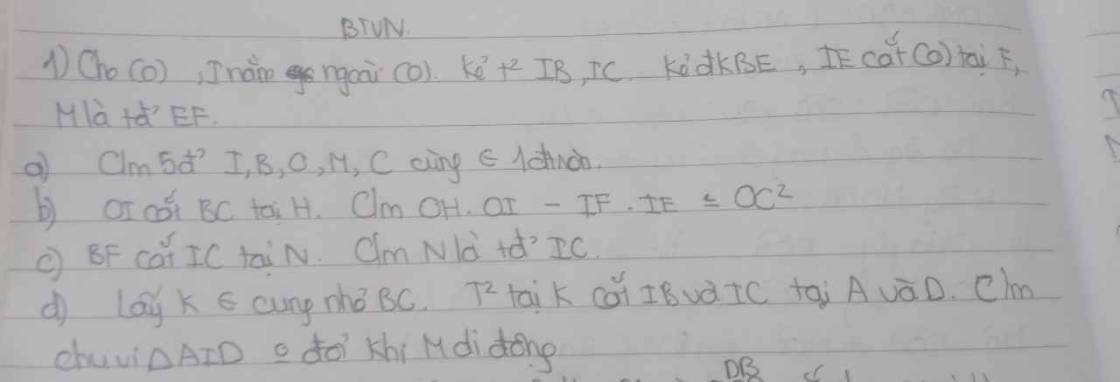
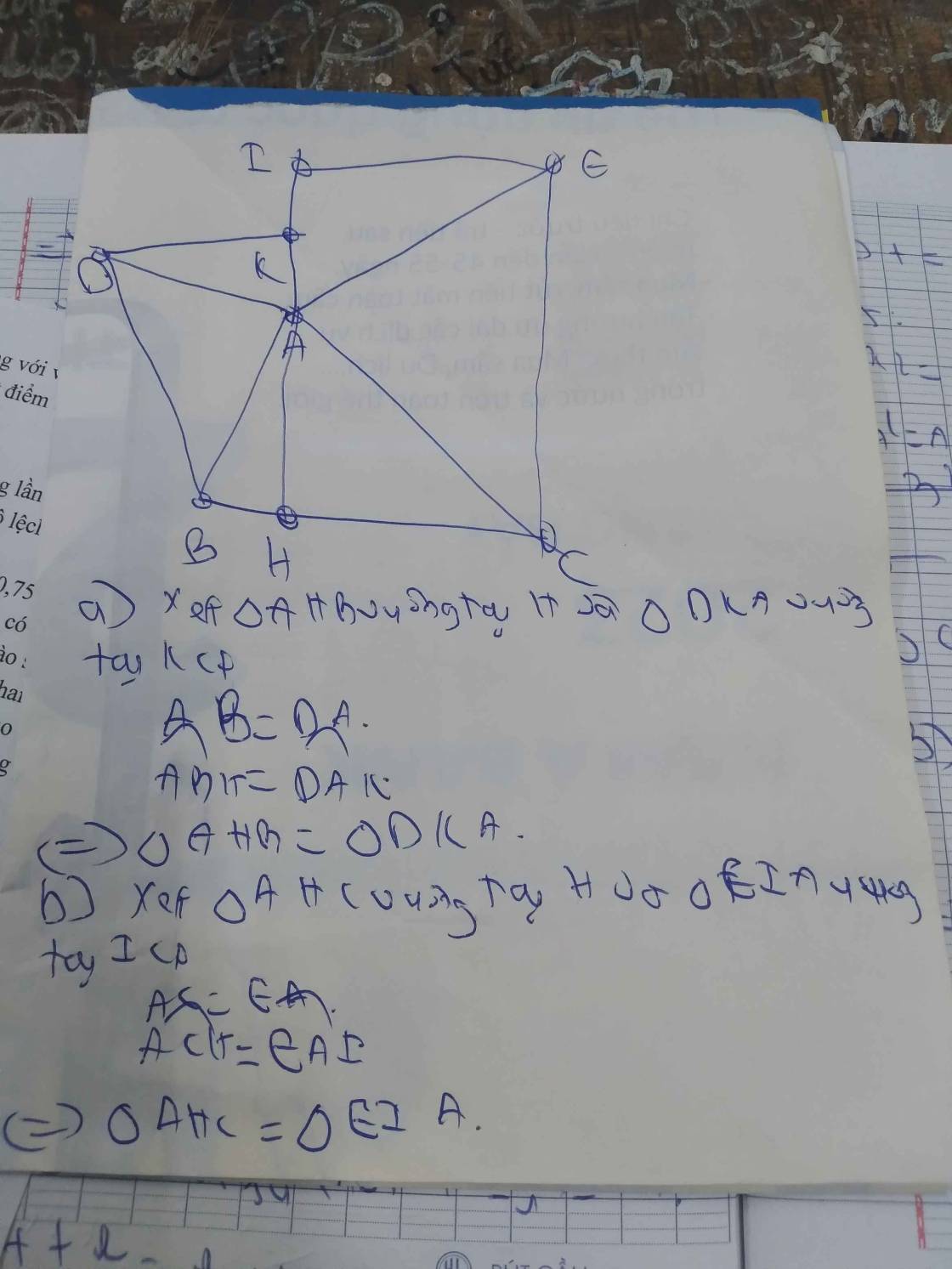
a: Ta có: ΔOEF cân tại O
mà OM là đường trung tuyến
nên OM\(\perp\)EF tại M
Ta có: \(\widehat{OMI}=\widehat{OCI}=\widehat{OBI}=90^0\)
=>O,M,I,C,B cùng thuộc đường tròn đường kính OI
d: Xét (O) có
AB,AK là các tiếp tuyến
Do đó: AB=AK
Xét (O) có
DK,DC là các tiếp tuyến
Do đó: DK=DC
Chu vi tam giác IAD là:
IA+AD+ID
=IA+AK+KD+ID
=IA+AB+DC+ID
=IB+IC
=2IB không đổi khi M di động
Đúng 1
Bình luận (0)
Làm bài 7 chi tiết ạ cả 2 càng tốt ạ
Bài 8:
a) \(x^2-25x=0\)
\(\Leftrightarrow x\left(x-25\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-25=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=25\end{matrix}\right.\)
b) \(7x\left(x-3\right)-5\left(3-x\right)=0\)
\(\Leftrightarrow7x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(7x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\7x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{7}\end{matrix}\right.\)
c) \(7x\left(x+4\right)-7x-28=0\)
\(\Leftrightarrow7x\left(x+4\right)-7\left(x+4\right)=0\)
\(\Leftrightarrow7\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\)
d) \(\left(2x^2+5x\right)\left(x^2-x\right)+\left(2x^2+10\right)\left(x-x^2\right)=0\)
\(\Leftrightarrow\left(2x^2+5x\right)\left(x^2-x\right)-\left(2x^2+10\right)\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x^2-x\right)\left(2x^2+5x-2x^2-10\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(5x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\5x-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (2)
7:
a: \(4a^3b-12a^2b^2+8ab^3\)
\(=4ab\cdot a^2-4ab\cdot3ab+4ab\cdot2b^2\)
\(=4ab\left(a^2-3ab+2b^2\right)\)
\(=4ab\left(a^2-ab-2ab+2b^2\right)\)
\(=4ab\left[a\left(a-b\right)-2b\left(a-b\right)\right]\)
\(=4ab\left(a-b\right)\left(a-2b\right)\)
b: \(\dfrac{5}{2}x^4+\dfrac{3}{4}x^3-\dfrac{1}{5}x^2\)
\(=x^2\cdot\dfrac{5}{2}x^2+x^2\cdot\dfrac{3}{4}x-x^2\cdot\dfrac{1}{5}\)
\(=x^2\left(\dfrac{5}{2}x^2+\dfrac{3}{4}x-\dfrac{1}{5}\right)\)
c: \(3x^2\left(x+9\right)-2\left(x+9\right)\)
\(=\left(x+9\right)\cdot3x^2-\left(x+9\right)\cdot2\)
\(=\left(x+9\right)\left(3x^2-2\right)\)
d: \(3x^2\left(7x+y\right)-5x\left(7x+y\right)+14x+2y\)
\(=\left(7x+y\right)\left(3x^2-5x\right)+2\left(7x+y\right)\)
\(=\left(7x+y\right)\left(3x^2-5x+2\right)\)
\(=\left(7x+y\right)\left(3x^2-3x-2x+2\right)\)
\(=\left(7x+y\right)\left[3x\left(x-1\right)-2\left(x-1\right)\right]\)
\(=\left(7x+y\right)\left(x-1\right)\left(3x-2\right)\)
Đúng 1
Bình luận (0)

Giúp mình bài này với ạ, chi tiết càng tốt ạ <3
a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Đúng 2
Bình luận (0)
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).
Đúng 1
Bình luận (0)
Mn ơi khoanh đáp án đúng và giải thích giúp mik với ạ ( giải thik càng chi tiết càng tốt, mik cảm ơn trc ạ)
12 C
13 A
14 A
15 C
16 A
17 B
18 D
19 B
20 A
21 D
Đúng 2
Bình luận (0)
Mn ơi khoanh đáp án đúng và giải thích giúp mik với ạ ( giải thik càng chi tiết càng tốt, mik cảm ơn trc ạ)
22. B
flexible: linh hoạt
rigid: cứng rắn
23. D
close to the bone: thiếu tinh tế, tôn trọng
respecful: tôn trọng
24. B
A: Chúc mừng!
B:Thật tuyệt với!
C: Tốt lắm!
D: Thật đáng tiếc!
25. C
A: Tôi có thể đề lại cho cô ấy 1 lời nhắn không ?
B: Vì tôi ra ngoài.
C: Linda đã không nghe điện thoại.
D: Để chạm tới cô ấy.
Đúng 1
Bình luận (0)