Giải tam giác DEF vuông tại D có DE=3cm, EF =5cm (số đo gốc làm tròn đến độ)
LH
Những câu hỏi liên quan
Cho tam giác vuông DEF vuông tại D có DE = 3cm DF = 4cm số đo góc E làm tròn đến độ là
Áp dụng tslg trong tam giác DEF vuông tại D:
\(tanE=\dfrac{DF}{DE}=\dfrac{4}{3}\Rightarrow\widehat{E}\approx53^0\)
Đúng 1
Bình luận (1)
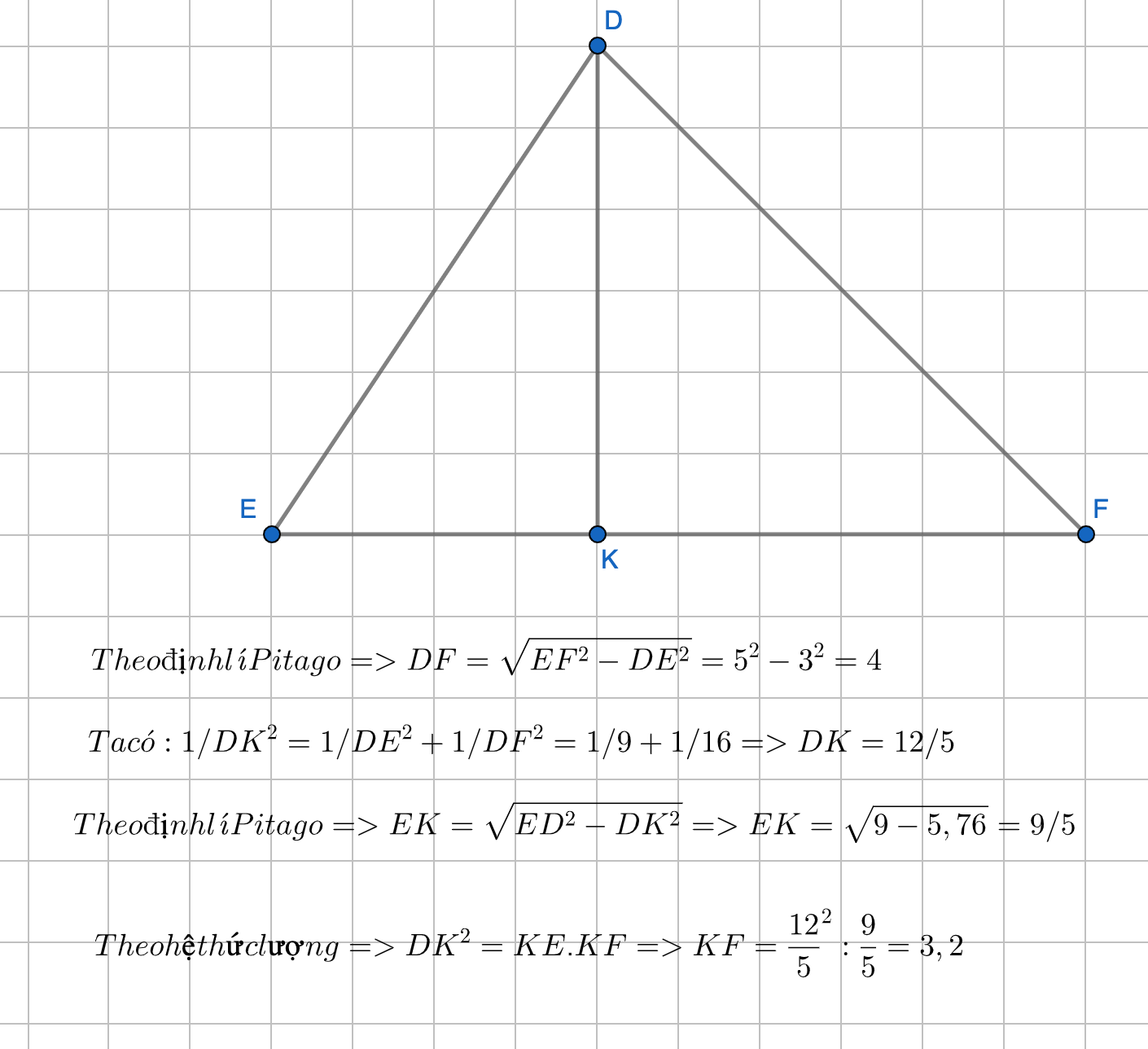
Cho tam giác DEF vuông tại D , có đường cao DK ; DE = 3cm , EF = 5cm . Tính EK , KF , DK.
Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(DE^2+DF^2=EF^2\)
\(\Leftrightarrow DF^2=5^2-3^2=16\)
hay DE=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDEF vuông tại D có DK là đường cao ứng với cạnh huyền EF, ta được:
\(DK\cdot FE=DE\cdot DF\)
\(\Leftrightarrow DK\cdot5=3\cdot4=12\)
hay DK=2,4(cm)
Áp dụng định lí Pytago vào ΔDKE vuông tại K, ta được:
\(DE^2=DK^2+EK^2\)
\(\Leftrightarrow EK^2=3^2-2.4^2=3.24\)
hay EK=1,8(cm)
Ta có: EK+FK=EF(K nằm giữa E và F)
nên FK=5-1,8=3,2(cm)
Đúng 3
Bình luận (0)
Áp dụng hệ thức lượng:
\(DE^2=EK.EF\Rightarrow EK=\dfrac{DE^2}{EF}=1,8\left(cm\right)\)
\(KF=EF-EK=3,2\left(cm\right)\)
\(DK^2=EK.KF\Rightarrow DK=\sqrt{EK.KF}=2,4\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác DEF cân tại D, có DE=DF=5cm, góc D=80 độ. Kẻ DH vuông góc với EF(H thuộc EF)
a) Tính số đo góc E
b) Chứng minh EH=HF và góc EDH=góc FDH
c) Tính EF. biết DH=4cm
d) Kẻ HM vuông góc với DE; HN vuông góc với DF. Chứng minh tam giác DMN là tam giác cân tại D
*Vẽ hình dùm mik luôn với!?-
Cho tam giác ABC vuông tại A có BC=2AB=2a. Gọi D là trung điểm của BC. Vẽ tam giác DEF vuông tại D có E thuộc AC, F thuộc AB.
a, Tính số đo các góc tam giác DEF
b, Tính diện tích tam giác DEF theo DE
c, Khi diện tích tam giác DEF nhỏ nhất, tính độ dài cung EF của đường tròn ngoại tiếp tam giác DEF
Cho tam giác ABC vuông tại A có BC=2AB=2a. Gọi D là trung điểm của BC. Vẽ tam giác DEF vuông tại D có E thuộc AC, F thuộc AB.
a, Tính số đo các góc tam giác DEF
b, Tính diện tích tam giác DEF theo DE
c, Khi diện tích tam giác DEF nhỏ nhất, tính độ dài cung EF của đường tròn ngoại tiếp tam giác DEF
Cho tam giác DEF vuông tại D, đường cao DH. Hãy tính lần lượt độ dài các đoạn EF,DH nếu biết:
a)DE=3cm; DF=4cm
b)DE=12cm;DF=9cm
c)DE=12cm;DF=5cm
a) \(EF=\sqrt{3^2+4^2}=5\)(cm)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}=2,4\left(cm\right)\)
b) \(EF=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cm\right)\)
c) \(EF=\sqrt{12^2+5^2}=13\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác MNP vuông tại M, có MN = 3cm, NP= 5cm. Giải tam giác vuông MNP ( góc làm tròn đến độ )
MP=4cm
\(\widehat{N}=53^0;\widehat{P}=37^0\)
Đúng 4
Bình luận (0)
cho tam giác DEF vuông tại có DE<DF.Gọi M là trung điểm EF. Biết DE=3cm, DF=4cm, FE=5cm. Tính DM.
Vì DM là trung tuyến ứng với cạnh huyền EF nên \(DM=\dfrac{1}{2}EF=\dfrac{5}{2}=2,5\left(cm\right)\)
Đúng 3
Bình luận (1)
cho tam giác def có de=3cm; df=5cm; ef = 4cm c/m tam giác def vuông . tính S tam giác DEF
ta thấy 3x3+4x4=5x5 nên nó là tam giác vuông
diện tích là S=1/2x3x4=6(cm2)
chúc bạn học tốt
HYC-23/1/2022