tìm max min
a) ( 2x + 1/3)^4 - 1
b) - (4/9x - 2/15) ^6 +3
TT
Những câu hỏi liên quan
a) Tìm Min của biểu thức A = ( 2x + 1/3)^4 - 1
b) Tìm Max của biểu thức B = -(4/9x - 2/15 ) ^ 6 + 3
a) Ta có: \(\left(2x+\frac{1}{3}\right)^4\ge0\)
\(\Rightarrow A=\left(2x+\frac{1}{3}\right)^4-1\ge-1\)
Vậy \(MIN_A=-1\) khi \(x=\frac{-1}{6}\)
b) Ta có: \(-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\le0\) ( do \(\left(\frac{4}{9}x-\frac{2}{15}\right)^6\ge0\) )
\(\Rightarrow B=-\left(\frac{4}{9}x-\frac{2}{15}\right)^6+3\le3\)
Vậy \(MAX_B=3\) khi \(x=\frac{3}{10}\)
Đúng 0
Bình luận (0)
Tìm
a) Min của A=(2x+1/3)4 -1
b) Max của B= -(4/9 .x -2/15)6 +3
a)Do \(\left(2x+\frac{1}{3}\right)^4\ge0\) => \(A\ge-1\)
Dấu "=" xảy ra khi \(2x+\frac{1}{3}=0=>2x=-\frac{1}{3}=>x=-\frac{1}{6}\)
Vậy Min A = -1 khi x = \(\frac{-1}{6}\)
b)Do \(-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\le0=>B\le3\)
Dấu "=" xảy ra khi \(\frac{4}{9}x-\frac{2}{15}=0=>\frac{4}{9}x=\frac{2}{15}=>x=\frac{3}{10}\)
Vậy Max B = 3 khi x = \(\frac{3}{10}\)
Đúng 0
Bình luận (0)
tìm min B=3|2x+4|-15
tìm max A=-|x-6|+24
B = 3 | 2x + 4 | - 15
Vì | 2x + 4 | \(\ge0\forall x\)
=> 3 | 2x + 4 | \(\ge0\forall x\)
=> 3 | 2x + 4 | - 15 \(\ge-15\forall x\)
=> B \(\ge-15\forall x\)
=> B = - 15 <=> | 2x + 4 | = 0
<=> 2x + 4 = 0
<=> 2x = - 4
<=> x = - 2
Vậy B min = - 15 khi x = - 2
A = - | x - 6 | + 24
Vì | x - 6 | \(\ge0\forall x\)
=> - | x - 6 | \(\le0\forall x\)
=> - | x - 6 | + 24 \(\le24\forall x\)
=> A \(\le24\forall x\)
=> A = 24 <=> | x - 6 | = 0
<=> x - 6 = 0
<=> x = 6
Vậy A max = 24 khi x = 6
Đúng 0
Bình luận (0)
Ta có \(\text{3|2x+4|}\ge0\Rightarrow\text{3|2x+4|}-15\ge15\)
Dấu "=" xảy ra khi \(\text{3|2x+4|=0\Rightarrow2}x+4=0\Rightarrow2x=-4\Rightarrow x=-2\)
Đúng 0
Bình luận (0)
Bài 1 Tìm Min hoặc Max
a)2x^2+10x-1
b) 5x - x^2
c) 2x^2-8x-10
d)9x-3x^2
Bài 2 Phân Tích x^4-2x^3-2x^2-2x-3
Bài 1 Tìm Min hoặc Max
a)2x^2+10x-1
b) 5x - x^2
c) 2x^2-8x-10
d)9x-3x^2
Bài 2 Phân Tích x^4-2x^3-2x^2-2x-3
Bài 1 : a) tìm min của A=(2x+1/3)^4-1
b)tìm max của B=-(4/9x-2/15)=2/7
Bài 2: a) tìm x biết (3x+3)^100+1 < hoặc = 0
b) tìm x biết (x-1)^x+2=(x-1)^x+4
Bài 3 : a)54^4 và 21^12
b )2^31 và 5^35
giải hộ em
a,Tìm min, max: 4x-16 căn x+4y-22 căn y-4 căn xy+36
b, tìm max :B= 6 cẵn+3/2x+4
c, Tìm Min : C=2/1-x+1/x
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
Đúng 0
Bình luận (0)
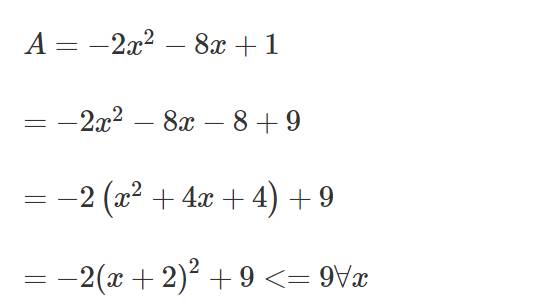
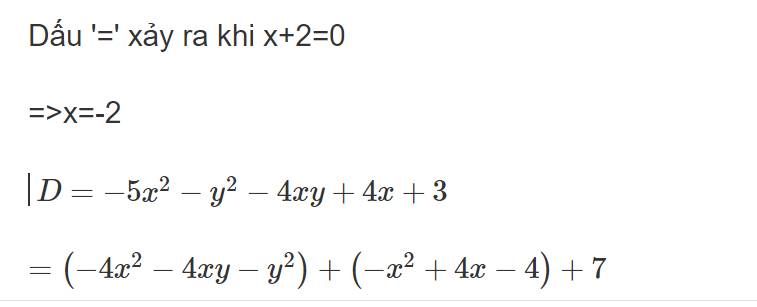
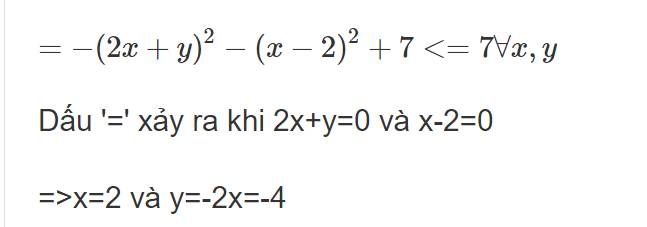
a. Tìm Min A = \(\left(2x+\frac{1}{3}\right)4-1\)
b. Tìm Max B = \(-\left(\frac{4}{9}x-\frac{2}{15}\right)^6+3\)
Giúp Thảo nhé !
Câu a hình như sai đề mk sửa nha
a)\(A=\left(2x+\frac{1}{3}\right)^4-1\)
Vì \(\left(2x+\frac{1}{3}\right)^4\ge0\)
Suy ra:\(\left(2x+\frac{1}{3}\right)^4-1\ge-1\)
Dấu = xảy ra khi \(2x+\frac{1}{3}=0\)
\(2x=-\frac{1}{3}\)
\(x=-\frac{1}{6}\)
Vậy Min A=-1 khi \(x=-\frac{1}{6}\)
Đúng 0
Bình luận (2)
b)\(B=-\left(\frac{4}{9}x-\frac{2}{15}\right)^6+3\)
\(B=3-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\)
Vì \(-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\le0\)
Suy ra:\(3-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\le3\)
Dấu = xảy ra khi \(\frac{4}{9}x-\frac{2}{15}=0\)
\(\frac{4}{9}x=\frac{2}{15}\)
\(x=\frac{3}{10}\)
Vậy Max B=3 khi \(x=\frac{3}{10}\)
Đúng 0
Bình luận (1)